山东省泰安市2021年中考数学试卷

修改时间：2024-07-13 浏览次数：381 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题（本大题共12小题，每小题选对得4分.）

1. 下列各数：﹣4，﹣2.8，0，|﹣4|，其中比﹣3小的数是（）

A . ﹣4 B . |﹣4| C . 0 D . ﹣2.8

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . 2x²+3x³＝5x⁵ B . （﹣2x）³＝﹣6x³ C . （x+y）²＝x²+y² D . （3x+2）（2﹣3x）＝4﹣9x²

查看解析收藏纠错

+选题
3. 如图是由若干个同样大小的小正方体所搭几何体的俯视图，小正方形中的数字表示在该位置小正方体的个数，则这个几何体的左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图，直线m∥n ，三角尺的直角顶点在直线m上，且三角尺的直角被直线m平分，若∠1＝60°，则下列结论错误的是（）

A . ∠2＝75° B . ∠3＝45° C . ∠4＝105° D . ∠5＝130°

查看解析收藏纠错

+选题
5. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，则所调查学生睡眠时间的众数，中位数分别为（）

A . 7h ， 7h B . 8h ， 7.5h C . 7h ， 7.5h D . 8h ， 8h

查看解析收藏纠错

+选题
6. 如图，在△ABC中，AB＝6，以点A为圆心，3为半径的圆与边BC相切于点D ，与AC ， AB分别交于点E和点G ，点F是优弧GE上一点，∠CDE＝18°，则∠GFE的度数是（）

A . 50° B . 48° C . 45° D . 36°

查看解析收藏纠错

+选题
7. 已知关于x的一元二次方程kx²﹣（2k﹣1）x+k﹣2＝0有两个不相等的实数根，则实数k的取值范围是（）

A . k＞﹣ $\text{[math]}$ B . k＜ $\text{[math]}$ C . k＞﹣ $\text{[math]}$ 且k≠0 D . k＜ $\text{[math]}$ 且k≠0

查看解析收藏纠错

+选题
8. 将抛物线y＝﹣x²﹣2x+3的图象向右平移1个单位，再向下平移2个单位得到的抛物线必定经过（）

A . （﹣2，2） B . （﹣1，1） C . （0，6） D . （1，﹣3）

查看解析收藏纠错

+选题
9. 如图，四边形ABCD是⊙O的内接四边形，∠B＝90°，∠BCD＝120°，AB＝2，CD＝1，则AD的长为（）

A . 2 $\text{[math]}$ ﹣2 B . 3﹣ $\text{[math]}$ C . 4﹣ $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
10. 如图，在平行四边形ABCD中，E是BD的中点，则下列四个结论：
①AM＝CN；②若MD＝AM ， ∠A＝90°，则BM＝CM；③若MD＝2AM ，则S_△_MNC＝S_△_BNE；④若AB＝MN ，则△MFN与△DFC全等．

其中正确结论的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
11. 如图，为了测量某建筑物BC的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，沿斜坡AD行走130米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为60°，建筑物底端B的俯角为45°，点A、B、C、D、E在同一平面内，斜坡AD的坡度i＝1：2.4．根据小颖的测量数据，计算出建筑物BC的高度约为（参考数据： $\text{[math]}$ ≈1.732）（）

A . 136.6米 B . 86.7米 C . 186.7米 D . 86.6米

查看解析收藏纠错

+选题
12. 如图，在矩形ABCD中，AB＝5，BC＝5 $\text{[math]}$ ，点P在线段BC上运动（含B、C两点），连接AP ，以点A为中心，将线段AP逆时针旋转60°到AQ ，连接DQ ，则线段DQ的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

查看解析收藏纠错

+选题

二、填空题（本大题共6小题，满分18分。）

13. 2021年5月15日7时18分，天问一号着陆巡视器成功着陆于火星，我国首次火星探测任务着陆火星取得圆满成功．探测器距离地球约3.2亿千米．数据3.2亿千米用科学记数法可以表示为千米．

查看解析收藏纠错

+选题
14. 《九章算术》中记载：“今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？”其大意是：“今有甲乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；而甲把其 $\text{[math]}$ 的钱给乙，则乙的钱数也为50．问甲、乙各有多少钱？”设甲的钱数为x ，乙的钱数为y ，根据题意，可列方程组为．

查看解析收藏纠错

+选题
15. 如图是抛物线y＝ax²+bx+c的部分图象，图象过点（3，0），对称轴为直线x＝1，有下列四个结论：①abc＞0；②a﹣b+c＝0；③y的最大值为3；④方程ax²+bx+c+1＝0有实数根．其中正确的为（将所有正确结论的序号都填入）．

查看解析收藏纠错

+选题
16. 若△ABC为直角三角形，AC＝BC＝4，以BC为直径画半圆如图所示，则阴影部分的面积为．

查看解析收藏纠错

+选题
17. 如图，将矩形纸片ABCD折叠（AD＞AB），使AB落在AD上，AE为折痕，然后将矩形纸片展开铺在一个平面上，E点不动，将BE边折起，使点B落在AE上的点G处，连接DE ，若DE＝EF ， CE＝2，则AD的长为．

查看解析收藏纠错

+选题
18. 如图，点B₁在直线l：y＝ $\text{[math]}$ x上，点B₁的横坐标为2，过点B₁作B₁A₁⊥l ，交x轴于点A₁ ，以A₁B₁为边，向右作正方形A₁B₁B₂C₁ ，延长B₂C₁交x轴于点A₂；以A₂B₂为边，向右作正方形A₂B₂B₃C₂ ，延长B₃C₂交x轴于点A₃；以A₃B₃为边，向右作正方形A₃B₃B₄C₃ ，延长B₄C₃交x轴于点A₄；…；照这个规律进行下去，则第n个正方形A_nB_nB_n₊₁∁_n的边长为（结果用含正整数n的代数式表示）．

查看解析收藏纠错

+选题

三、解答题（本大题共7小题，满分78分.）

19.

（1）先化简，再求值： $\text{[math]}$ ，其中a＝ $\text{[math]}$ +3；

（2）解不等式：1﹣ $\text{[math]}$ ．

查看解析收藏纠错

+选题

20. 为庆祝中国共产党成立100周年，落实教育部《关于在中小学组织开展“从小学党史，永远跟党走”主题教育活动的通知》要求，某学校举行党史知识竞赛，随机调查了部分学生的竞赛成绩，绘制成两幅不完整的统计图表．根据统计图表提供的信息，解答下列问题：

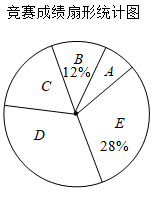
竞赛成绩统计表（成绩满分100分）

组别	分数	人数
A组	75＜x≤80	4
B组	80＜x≤85
C组	85＜x≤90	10
D组	90＜x≤95
E组	95＜x≤100	14
合计

（1）本次共调查了名学生；C组所在扇形的圆心角为度；

（2）该校共有学生1600人，若90分以上为优秀，估计该校优秀学生人数为多少？

（3）若E组14名学生中有4人满分，设这4名学生为E1，E2，E3，E4，从其中抽取2名学生代表学校参加上一级比赛，请用列表或画树状图的方法求恰好抽到E1，E2的概率．

查看解析收藏纠错

+选题

21. 如图，点P为函数y＝ $\text{[math]}$ x+1与函数y＝ $\text{[math]}$ （x＞0）图象的交点，点P的纵坐标为4，PB⊥x轴，垂足为点B ．

（1）求m的值；

（2）点M是函数y＝ $\text{[math]}$ （x＞0）图象上一动点，过点M作MD⊥BP于点D ，若tan∠PMD＝ $\text{[math]}$ ，求点M的坐标．

查看解析收藏纠错

+选题
22. 接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂．为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂．

（1）求该厂当前参加生产的工人有多少人？

（2）生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时．若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？

查看解析收藏纠错

+选题
23. 四边形ABCD为矩形，E是AB延长线上的一点．

（1）若AC＝EC ，如图1，求证：四边形BECD为平行四边形；

（2）若AB＝AD ，点F是AB上的点，AF＝BE ， EG⊥AC于点G ，如图2，求证：△DGF是等腰直角三角形．

查看解析收藏纠错

+选题
24. 二次函数y＝ax²+bx+4（a≠0）的图象经过点A（﹣4，0），B（1，0），与y轴交于点C ，点P为第二象限内抛物线上一点，连接BP、AC ，交于点Q ，过点P作PD⊥x轴于点D ．

（1）求二次函数的表达式；

（2）连接BC ，当∠DPB＝2∠BCO时，求直线BP的表达式；

（3）请判断： $\text{[math]}$ 是否有最大值，如有请求出有最大值时点P的坐标，如没有请说明理由．

查看解析收藏纠错

+选题
25. 如图1，O为半圆的圆心，C、D为半圆上的两点，且 $\text{[math]}$ ．连接AC并延长，与BD的延长线相交于点E ．

（1）求证：CD＝ED；

（2） AD与OC ， BC分别交于点F ， H ．
①若CF＝CH ，如图2，求证：CF•AF＝FO•AH；

②若圆的半径为2，BD＝1，如图3，求AC的值．

查看解析收藏纠错

+选题

山东省泰安市2021年中考数学试卷

一、选择题（本大题共12小题，每小题选对得4分.）

二、填空题（本大题共6小题，满分18分。）

三、解答题（本大题共7小题，满分78分.）

相关试卷 收起∨

相关试卷收起∨