湖南省湘西市2020年中考数学试卷

修改时间：2021-05-20 浏览次数：352 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列各数中，比 $\text{[math]}$ 小的数是（）

A . 0 B . -1 C . -3 D . 3

查看解析收藏纠错

+选题
2. 2019年中国与“一带一路”沿线国家货物贸易进出口总额达到92700亿元．用科学记数法表示92700是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图是由4个相同的小正方体组成的一个水平放置的立体图形，其箭头所指方向为主视方向，其俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 从长度分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四条线段中随机取出三条，则能够组成三角形的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 已知 $\text{[math]}$ ，作 $\text{[math]}$ 的平分线 $\text{[math]}$ ，在射线 $\text{[math]}$ 上截取线段 $\text{[math]}$ ，分别以O、C为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧相交于E，F．画直线 $\text{[math]}$ ，分别交 $\text{[math]}$ 于D，交 $\text{[math]}$ 于G．那么， $\text{[math]}$ 一定是（）

A . 锐角三角形 B . 钝角三角形 C . 等腰三角形 D . 直角三角形

查看解析收藏纠错

+选题
7. 已知正比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，下列说法正确的是（）

A . 正比例函数 $\text{[math]}$ 的解析式是 $\text{[math]}$ B . 两个函数图象的另一交点坐标为 $\text{[math]}$ C . 正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 都随x的增大而增大 D . 当 $\text{[math]}$ 或 $\text{[math]}$ 时， $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图， $\text{[math]}$ 、 $\text{[math]}$ 为⊙O的切线，切点分别为A、B， $\text{[math]}$ 交 $\text{[math]}$ 于点C， $\text{[math]}$ 的延长线交⊙O于点D．下列结论不一定成立的是（）

A . $\text{[math]}$ 为等腰三角形 B . $\text{[math]}$ 与 $\text{[math]}$ 相互垂直平分 C . 点C、B都在以 $\text{[math]}$ 为直径的圆上 D . $\text{[math]}$ 为 $\text{[math]}$ 的边 $\text{[math]}$ 上的中线

查看解析收藏纠错

+选题
9. 如图，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的顶点A在x轴的正半轴上，矩形的另一个顶点D在y轴的正半轴上，矩形的边 $\text{[math]}$ ．则点C到x轴的距离等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 已知二次函数 $\text{[math]}$ 图象的对称轴为 $\text{[math]}$ ，其图象如图所示，现有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ．正确的是（）

A . ①③ B . ②⑤ C . ③④ D . ④⑤

查看解析收藏纠错

+选题

二、填空题

11. - $\text{[math]}$ 的绝对值是。

查看解析收藏纠错

+选题
12. 分解因式： $\text{[math]}$ =．

查看解析收藏纠错

+选题
13. 若多边形的内角和是外角和的2倍，则该多边形是边形.

查看解析收藏纠错

+选题
14. 不等式组 $\text{[math]}$ 的解集为．

查看解析收藏纠错

+选题
15. 如图，直线 $\text{[math]}$ ∥ $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 度．

查看解析收藏纠错

+选题
16. 从甲、乙两种玉米种子中选择一种合适的推荐给某地．考虑到庄稼人对玉米的产量和产量的稳定性十分的关心，选择之前，为了解甲、乙两种玉米种子的情况，某单位各用了10块自然条件相同的试验田进行试验，得到各试验田每公顷产量（单位：t）的数据，这两组数据的平均数分别是 $\text{[math]}$ _甲 $\text{[math]}$ ， $\text{[math]}$ _乙 $\text{[math]}$ ，方差分别是 $\text{[math]}$ 2甲 $\text{[math]}$ 2乙 $\text{[math]}$ ，你认为应该选择的玉米种子是．

查看解析收藏纠错

+选题
17. 在平面直角坐标系中，O为原点，点 $\text{[math]}$ ，点B在y轴的正半轴上， $\text{[math]}$ ．矩形 $\text{[math]}$ 的顶点D，E，C分别在 $\text{[math]}$ 上， $\text{[math]}$ ．将矩形 $\text{[math]}$ 沿x轴向右平移，当矩形 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分的面积为 $\text{[math]}$ 时，则矩形 $\text{[math]}$ 向右平移的距离为．

查看解析收藏纠错

+选题
18. 观察下列结论：
⑴如图①，在正三角形 $\text{[math]}$ 中，点M，N是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；

⑵如图②，在正方形 $\text{[math]}$ 中，点M，N是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；

⑶如图③，在正五边形 $\text{[math]}$ 中，点M，N是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；……

根据以上规律，在正n边形 $\text{[math]}$ 中，对相邻的三边实施同样的操作过程，即点M，N是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于O．也会有类似的结论．你的结论是．

查看解析收藏纠错

+选题

三、解答题

19. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 化简： $\text{[math]}$ ．

查看解析收藏纠错

+选题
21. 如图，在正方形 $\text{[math]}$ 的外侧，作等边角形 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）求 $\text{[math]}$ 的度数．

查看解析收藏纠错

+选题
22. 为加强安全教育，某校开展了“防溺水”安全知识竞赛，想了解七年级学生对“防溺水”安全知识的掌握情况．现从七年级学生中随机抽取50名学生进行竞赛，并将他们的竞赛成绩（百分制）进行整理、描述和分析．部分信息如下：
a．七年级参赛学生成绩频数分布直方图（数据分成五组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）如图所示

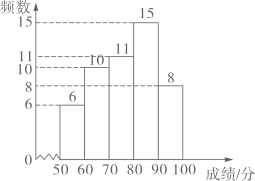
b．七年级参赛学生成绩在 $\text{[math]}$ 这一组的具体得分是：70，71，73，75，76，76，76，77，77，78 ，79

c．七年级参赛学生成绩的平均数、中位数、众数如下：

年级

平均数

中位数

众数

七

76.9

m

80

d．七年级参赛学生甲的竞赛成绩得分为79分．

根据以上信息，回答下列问题：

（1）在这次测试中，七年级在75分以上（含75分）的有人；

（2）表中m的值为；

（3）在这次测试中，七年级参赛学生甲的竞赛成绩得分排名年级第名；

（4）该校七年级学生有500人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．

查看解析收藏纠错

+选题
23. 某口罩生产厂生产的口罩1月份平均日产量为20000，1月底因突然爆发新冠肺炎疫情，市场对口罩需求量大增，为满足市场需求，工厂决定从2月份起扩大产能，3月份平均日产量达到24200个．

（1）求口罩日产量的月平均增长率；

（2）按照这个增长率，预计4月份平均日产量为多少？

查看解析收藏纠错

+选题
24. 如图， $\text{[math]}$ 是⊙O的直径， $\text{[math]}$ 是⊙O的切线， $\text{[math]}$ 交⊙O于点E．

（1）若D为 $\text{[math]}$ 的中点，证明： $\text{[math]}$ 是⊙O的切线；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求⊙O的半径 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
25. 如图

（1）问题背景：如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 绕B点旋转，它的两边分别交 $\text{[math]}$ 、 $\text{[math]}$ 于E、F．探究图中线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．小李同学探究此问题的方法是：延长 $\text{[math]}$ 到G，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得出结论，他的结论就是；

（2）探究延伸1：如图2，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 绕B点旋转，它的两边分别交 $\text{[math]}$ 、 $\text{[math]}$ 于E、F．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由．

（3）探究延伸2：如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 绕B点旋转，它的两边分别交 $\text{[math]}$ 、 $\text{[math]}$ 于E、F．上述结论是否仍然成立？并说明理由．

（4）实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西 $\text{[math]}$ 的A处舰艇乙在指挥中心南偏东 $\text{[math]}$ 的B处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东 $\text{[math]}$ 的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处，且指挥中心观测两舰艇视线之间的夹角为 $\text{[math]}$ ，试求此时两舰艇之间的距离．

查看解析收藏纠错

+选题
26. 已知直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ （b，c为常数， $\text{[math]}$ ）的一个交点为 $\text{[math]}$ ，点 $\text{[math]}$ 是x轴正半轴上的动点．

（1）当直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ （b，c为常数， $\text{[math]}$ ）的另一个交点为该抛物线的顶点E时，求k，b，c的值及抛物线顶点E的坐标；

（2）在（1）的条件下，设该抛物线与y轴的交点为C，若点Q在抛物线上，且点Q的横坐标为b，当 $\text{[math]}$ 时，求m的值；

（3）点D在抛物线上，且点D的横坐标为 $\text{[math]}$ ，当 $\text{[math]}$ 的最小值多 $\text{[math]}$ 时，求b的值．

查看解析收藏纠错

+选题

年级	平均数	中位数	众数
七	76.9	m	80

湖南省湘西市2020年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨