广东省广州市2019届高三理数第二次模拟考试试卷

修改时间：2024-07-13 浏览次数：462 类型：高考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 已知复数 $\text{[math]}$ 在复平面内对应的点在第三象限，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 已如集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
3. 某公司生产 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种不同型号的轿车，产量之比依次为 $\text{[math]}$ ，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为 $\text{[math]}$ 的样本，若样本中 $\text{[math]}$ 种型号的轿车比 $\text{[math]}$ 种型号的轿车少8辆，则 $\text{[math]}$ （）

A . 96 B . 72 C . 48 D . 36

查看解析收藏纠错

+选题
4. 执行如图所示的程序框图，则输出 $\text{[math]}$ 的值是（）

A . 21 B . 22 C . 23 D . 24

查看解析收藏纠错

+选题
5. 已知点 $\text{[math]}$ 与点 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动.设所选3人中女生人数为 $\text{[math]}$ ，则数学期望 $\text{[math]}$ （）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
7. 已知 $\text{[math]}$ ，其中 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 过双曲线 $\text{[math]}$ $\text{[math]}$ 的左焦点 $\text{[math]}$ 作圆 $\text{[math]}$ 的切线，切点为 $\text{[math]}$ ，延长 $\text{[math]}$ 交双曲线右支于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 若曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程为 $\text{[math]}$ ，且点 $\text{[math]}$ 在直线 $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ ）上，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 函数 $\text{[math]}$ $\text{[math]}$ 的部分图像如图所示，先把函数 $\text{[math]}$ 图像上各点的横坐标缩短到原来的 $\text{[math]}$ 倍，纵坐标不变，再把得到的图像向右平移 $\text{[math]}$ 个单位长度，得到函数 $\text{[math]}$ 的图像，则函数 $\text{[math]}$ 的图像的一条对称轴为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 已知点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ 的中点为 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
12. 若点 $\text{[math]}$ 与曲线 $\text{[math]}$ 上点 $\text{[math]}$ 的距离的最小值为 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 若 $\text{[math]}$ ， $\text{[math]}$ 是夹角为 $\text{[math]}$ 的两个单位向量，向量 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 若 $\text{[math]}$ 的展开式中 $\text{[math]}$ 的系数是80，则实数 $\text{[math]}$ 的值是.

查看解析收藏纠错

+选题
15. 秦九韶是我国南宋著名数学家，在他的著作《数书九章》中有已知三边求三角形面积的方法：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上.以小斜幂乘大斜幂减上，余四约之，为实.一为从隅，开平方得积.”如果把以上这段文字写成公式就是 $\text{[math]}$ ，共中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的内角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边为.若 $\text{[math]}$ ，且 $\text{[math]}$ ，1， $\text{[math]}$ 成等差数列，则 $\text{[math]}$ 面积 $\text{[math]}$ 的最大值为.

查看解析收藏纠错

+选题
16. 有一个底面半径为 $\text{[math]}$ ，轴截面为正三角形的圆锥纸盒，在该纸盒内放一个棱长均为 $\text{[math]}$ 的四面体，并且四面体在纸盒内可以任意转动，则 $\text{[math]}$ 的最大值为.

查看解析收藏纠错

+选题

三、解答题

17. 已知 $\text{[math]}$ 是递增的等比数列， $\text{[math]}$ ， $\text{[math]}$ .

（1）求数列 $\text{[math]}$ 的通项公式；

（2）令 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .

查看解析收藏纠错

+选题

18. 科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如下表：

$\text{[math]}$ （年龄/岁）	26	27	39	41	49	53	56	58	60	61
$\text{[math]}$ （脂肪含量/%）	14.5	17.8	21.2	25.9	26.3	29.6	31.4	33.5	35.2	34.6

根据上表的数据得到如下的散点图.

（1）根据上表中的样本数据及其散点图：

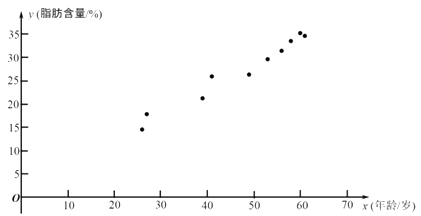
（i）求 $\text{[math]}$ ；

（i）计算样本相关系数（精确到0.01），并刻画它们的相关程度.

（2）若 $\text{[math]}$ 关于 $\text{[math]}$ 的线性回归方程为 $\text{[math]}$ ，求 $\text{[math]}$ 的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量.

附：参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，

参考公式：相关系数 $\text{[math]}$ $\text{[math]}$

回归方程 $\text{[math]}$ 中斜率和截距的最小二乘估计公式分别为 $\text{[math]}$ ， $\text{[math]}$ .

查看解析收藏纠错

+选题

19. 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 为菱形， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ .

（1）求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求二面角 $\text{[math]}$ 的余弦值.

查看解析收藏纠错

+选题
20. 在平面直角坐标系中，动点 $\text{[math]}$ 分别与两个定点 $\text{[math]}$ ， $\text{[math]}$ 的连线的斜率之积为 $\text{[math]}$ .

（1）求动点 $\text{[math]}$ 的轨迹 $\text{[math]}$ 的方程；

（2）设过点 $\text{[math]}$ 的直线与轨迹 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，判断直线 $\text{[math]}$ 与以线段 $\text{[math]}$ 为直径的圆的位置关系，并说明理由.

查看解析收藏纠错

+选题
21. 已知函数 $\text{[math]}$ $\text{[math]}$ .

（1）讨论函数 $\text{[math]}$ 的单调性；

（2）若函数 $\text{[math]}$ 有两个零点 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围，并证明 $\text{[math]}$ .

查看解析收藏纠错

+选题
22. 在直角坐标系 $\text{[math]}$ 中，倾斜角为 $\text{[math]}$ 的直线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 为参数）.在以坐标原点为极点， $\text{[math]}$ 轴正半轴为极轴的极坐标系中，曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ .

（1）求直线 $\text{[math]}$ 的普通方程与曲线 $\text{[math]}$ 的直角坐标方程；

（2）若直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，且 $\text{[math]}$ ，求直线 $\text{[math]}$ 的倾斜角.

查看解析收藏纠错

+选题
23. 已知函数 $\text{[math]}$ ．

（1）当 $\text{[math]}$ 时，解不等式 $\text{[math]}$ ；

（2）若存在实数x，使得 $\text{[math]}$ 成立，求实数a的取值范围.

查看解析收藏纠错

+选题

广东省广州市2019届高三理数第二次模拟考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨