题型:综合题 题类:模拟题 难易度:困难
湖南省长沙市开福区十校2021年初中学生学业水平联考数学试卷
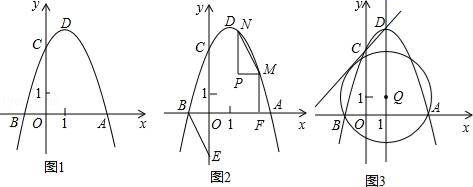
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.
已知抛物线y=x²-4x+3.
(1)该抛物线的对称轴是 , 顶点坐标 ;
(2)将该抛物线向上平移2个单位长度,再向左平移3个单位长度得到新的二次函数图象,请写出相应的解析式,并用列表,描点,连线的方法画出新二次函数的图象;
| x | … | … | |||||
| y | … | … |

(3)新图像上两点A(x1 , y1),B(x2 , y2),它们的横坐标满足x1<-2,且-1<x2<0,试比较y1 , y2 , 0三者的大小关系.
试题篮