2022年中考数学二轮专题复习-数据搜集整理数据分析概率

修改时间：2022-04-18 浏览次数：146 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 要调查本校学生学业负担是否过重，选用下列哪种方法最恰当?（）

A . 查阅文献资料 B . 对学生问卷调查 C . 上网查询 D . 对校领导问卷调查

查看解析收藏纠错

+选题
2. 为全面掌握小区居民新冠疫苗接种情况，社区工作人员设计了以下几种调查方案：
方案一：调查该小区每栋居民楼的10户家庭成员的疫苗接种情况；
方案二：随机调查该小区100位居民的疫苗接种情况；
方案三：对本小区所有居民的疫苗接种情况逐一调查统计．
在上述方案中，能较好且准确地得到该小区居民疫苗接种情况的是（）

A . 方案一 B . 方案二 C . 方案三 D . 以上都不行

查看解析收藏纠错

+选题
3. 植物园中有红豆杉、马尾松，长白松﹑银杏四种国家级保护植物，为了解本班同学喜欢哪种植物的人最多，需要进行调查，则调查的对象是（）

A . 本班的每一名同学 B . 红豆杉、马尾松、长白松.银杏 C . 同学们的选票 D . 记录下来的数据

查看解析收藏纠错

+选题
4. 如图，有4张形状大小质地均相同的卡片，正面印有速度滑雪．雪橇、冰壶、冬季两项等四种不同的图案，背面完全相同：

现将这4张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面恰好是冰壶项目图案的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 一组数据3、4、4、5，若添加一个数4后得到一组新数据，则前后两组数据的统计量会发生变化的是（　　）

A . 平均数 B . 众数 C . 中位数 D . 方差

查看解析收藏纠错

+选题
6. 为了向建党一百周年献礼，我市中小学生开展了“红色经典故事”主题演讲比赛。某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（）

A . 众数是82 B . 中位数是84 C . 方差是84 D . 平均数是85

查看解析收藏纠错

+选题
7. 九年级(1)班在参加学校4×100m接力赛时，安排了甲、乙、丙、丁四位同学，他们的顺序由抽签随机决定，则甲同学跑第一棒的概率为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 当今，大数据、云计算、人工智能等互联网新技术正在全方位改写中国社会，习近平总书记倡导的构建网络空间命运共同体的“五点主张”，已成为国际社会的广泛共识．而5G应用将是推动互联网这个“最大变量”变成“最大增量”的新引擎，5G的出现将改变中国的经济格局，据预测，2020年到2030年中国5G直接经济产出和间接经济产出的情况如图所示，根据图提供的信息，下列推断不合理的是（）

A . 2020年到2030年，5G直接经济产出和5G间接经济产出都是逐年增长 B . 2023年到2024年与2028年到2029年5G间接经济产出的增长率相同 C . 2027年5G间接经济产出比5G直接经济产出多3.4万亿 D . 2028年5G直接经济产出为2020年5G直接经济产出的9倍

查看解析收藏纠错

+选题
9. 为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数直方图(每组数据包含最小值，不包含最大值)，则仰卧起坐次数在25次(含25次)以上的人数共有（）

A . 10人 B . 12人 C . 17人 D . 都不对

查看解析收藏纠错

+选题
10. 某校为了了解全校学生对“智能杭州”的了解程度，随机抽取了部分学生进行问卷调查，并根据收集的信息进行了统计，绘制了下面尚不完整的统计图.根据以上的信息，给出下列判断：①参加问卷调查的学生有50人；②参加问卷调查的学生中，“基本了解”的有10人；③扇形图中“基本了解”部分的扇形的圆心角的度数是108°；④在参加问卷调查的学生中，“了解”的学生人数占10%.其中结论正确的序号是（）

A . ①②③ B . ①②④ C . ①③④ D . ②③④

查看解析收藏纠错

+选题
11. 5月1日至7日，我市每日最高气温如图所示，则下列说法错误的是（）
5月1日至7日最高气温统计图

A . 中位数是 $\text{[math]}$ B . 众数是 $\text{[math]}$ C . 平均数是 $\text{[math]}$ D . 4日至5日最高气温下降幅度较大

查看解析收藏纠错

+选题
12. 在如图所示的电路中，随机闭合开关S₁、S₂、S₃中的两个，能让灯泡L₁发光的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
13. 小明根据演讲比赛中9位评委所给的分数制作了如下表格：

平均数

中位数

众数

方差

8.0

8.2

8.3

0.2

如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

查看解析收藏纠错

+选题
14. 一个不透明的口袋中有三个完全相同的小球，把它们分别标号1、2、3，随机摸出一个小球不放回，再随机摸出一个小球，两次摸出的小球标号之和为5的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
15. 育种小组对某品种小麦发芽情况进行测试，在测试条件相同的情况下，得到如下数据：
抽查小麦粒数
100
300
800
1000
2000
3000
发芽粒数
96
287
770
958
1923
a
则a的值最有可能是（）

A . 2700 B . 2780 C . 2880 D . 2940

查看解析收藏纠错

+选题
16. 将一枚飞镖投掷到如图所示的正六边形镖盘上（每次飞镖均落在镖盘上，且落在镖盘的任何一个点的机会都相等），飞镖落在阴影区域的概率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
17. 下列说法正确的是（　　）.
①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．

A . ①② B . ②③ C . ③④ D . ①③

查看解析收藏纠错

+选题
18.
在学习掷硬币的概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是 ”，小明做了下列三个模拟实验来验证．
①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值；
②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值；
③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥（如图），从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值．上面的实验中，不科学的有（　　）.

A . 0个 B . 1个 C . 2个 D . 3个

查看解析收藏纠错

+选题
19.
如图，正方形ABCD内接于⊙O，⊙O的直径为 $\text{[math]}$ 分米，若在这个圆面上随意抛一粒豆子，则豆子落在正方形ABCD内的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

20. 下表选自北京师范大学出版社出版的《数学》课本（九年级下册）．

全国能源消费总量及其构成统计表

年份	能源消费总量/万吨标准煤	能源消费构成/%
年份	能源消费总量/万吨标准煤	原煤	原油	天然气	水电
1993	115993	74.7	18.2	1.9	5.2
1994	122737	75.0	17.4	1.9	5.7
1995	131176	74.6	17.5	1.8	6.1
1996	138948	74.7	18.0	1.8	5.5
1997	138173	71.5	20.4	1.7	6.2
1998	132214	69.6	21.5	2.2	6.7

全国能源生产总量及其构成统计表

年份	能源生产总量/万吨标准煤	能源生产结构/%
年份	能源生产总量/万吨标准煤	原煤	原油	天然气	水电
1993	111059	74.0	18.7	2.0	5.3
1994	118729	74.6	17.6	1.9	5.9
1995	129034	75.3	16.6	1.9	6.2
1996	132616	75.2	17.0	2.0	5.8
1997	132410	74.1	17.3	2.1	6.5
1998	124250	71.9	18.5	2.5	7.1

下列说法：

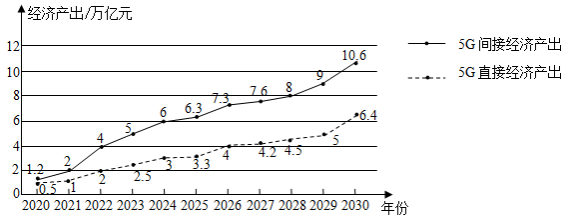
①从1993到1998年，能源消费总量和能源生产总量的变化趋势是一致的；

②从1993到1998年，能源消费总量和能源生产总量中，原煤所占比例越来越少；

③1998年和1997年相比，水电消费总量的增长率是0.5%；

④从1993到1998年，能源生产中，天然气生产总量越来越多．

其中正确的是（）

A . ①③ B . ①④ C . ③④ D . ①②

查看解析收藏纠错

+选题

二、填空题

21. 如图是4个外观完全相同的试剂瓶，分别装有稀硫酸溶液、稀盐酸溶液、氯化钠溶液、碳酸钠溶液．随机从这4瓶无标签试剂中抽取1瓶，抽到稀硫酸溶液的概率是．

查看解析收藏纠错

+选题

22. 十一国庆期间，小明爸爸从金塘收费站出发到舟山市人民政府办事，导航显示有两条路径可以选择，L₁：经过东西快速路；L₂：经过海天大道。据统计，通过两条路径所用的时间互不影响所用时间，所用时间落在各时间段内的频率如下表：（由公路部门根据当天统计）小明爸爸只有55分钟时间用于赶往目的地，请问他会选择路径．（填L₁或L₂）

时间（分）	35~40	40~50	45~50	50~55	55~60
L₁的频率	0.1	0.2	0.2	0.3	0.2
L₂的频率	0	0.1	0.5	0.3	0.1

查看解析收藏纠错

+选题

23. 小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是 $\text{[math]}$ ， $\text{[math]}$ ，那么两人中射击成绩比较稳定的是.

查看解析收藏纠错

+选题
24. 下图的扇形图是对某班学生知道父母生日情况的调查，A表示只知道父亲生日，B表示只知道母亲生日，C表示知道父母两人的生日，D表示父母生日都不知道.若该班有40名学生，则知道母亲生日的人数是.

查看解析收藏纠错

+选题
25. 古人云：“入门须正，立志须高”，人生目标选择非常重要.哈佛大学对一群智力、学历相似的人进行的“25年跟踪”发现：有清晰长期目标的人占3%，大都成了顶尖成功人士；有清晰短期目标的人占10%，大都成了顶尖专业人士；目标模糊者占60%，他们能安稳工作生活，无特别成绩；其余是无目标的人，经常失业，生活动荡.这一结果用扇形统计图表示如图所示，其中无目标的人所对应的扇形的圆心角的度数为.

查看解析收藏纠错

+选题
26. 某校七年级三个班男生人数与女生人数的比为3：2，各班的男、女学生人数统计图如图所示，则2班的学生人数是.

查看解析收藏纠错

+选题
27. 已知数据 $\text{[math]}$ 的平均数是 $\text{[math]}$ ，且 $\text{[math]}$ $\text{[math]}$ ，则数据 $\text{[math]}$ 的平均数和中位数分别是.

查看解析收藏纠错

+选题
28. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，实验数据如下表：
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率 $\text{[math]}$
0.58
0.64
0.58
0.59
0.605
0.601
根据数据，估计袋中黑球有个．

查看解析收藏纠错

+选题
29. 已知a、b、c、满足 $\text{[math]}$ ，从下列四点：① $\text{[math]}$ ；②(2，1)；③ $\text{[math]}$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

查看解析收藏纠错

+选题
30. 如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为．

查看解析收藏纠错

+选题

三、解答题

31. 今年5月11日至12日，习近平总书记考察山西时指出，“要加强社区建设和管理，加强社区环境整治……，增强太原人民的获得感、幸福感、安全感”.随后，全市上下认真学习和贯彻这一重要指示精神，掀起了创建全国文明城市的高潮，学校学生会和校团委积极响应招募志愿者参加每周日进社区服务活动，小王、小华、小亮、小明四名同学主动报名，随机组成两个小组（每组各两人），到最近的两个社区进行服务，求小王和小华去同一个社区服务的概率.（画树状图或列表时，可用字母W，H，L，M分别代表小王、小华、小亮、小明四名同学）

查看解析收藏纠错

+选题
32. 我国新冠灭活疫苗主要来自三家生物制品公司，分别是A：科兴中维、B：北京所、C：武汉所．灭活疫苗一般需要接种2针，假如一人两次接种的疫苗的生产公司随机，请你用列表或树状图的方法求出一个人两次接种的疫苗刚好是同一家公司生产的概率．

查看解析收藏纠错

+选题
33. 一个不透明的袋中装有2个红球、1个白球，这些球除颜色外，没有任何其他区别．有如下两个活动：
活动1：从袋中随机摸出一个球，记录下颜色，然后从袋中剩余的球中再随机摸出一个球，摸出的两个球都是红球的概率记为 $\text{[math]}$ ；
活动2：从袋中随机摸出一个球，记录下颜色，然后把这个球放回袋中并摇匀，重新从袋中随机摸出一个球，两次摸出的球都是红球的概率记为 $\text{[math]}$ ．
请你猜想 $\text{[math]}$ ， $\text{[math]}$ 的大小关系，并用画树状图或列表的方法列出所有可能的结果，验证你的猜想．

查看解析收藏纠错

+选题
34. 某校九年级（1）班的一个数学学习小组对全班某次测试中的“一道满分值为6分的解答题得分”情况进行了统计，绘制成下列不完整的统计图（学生得分均为整数）：

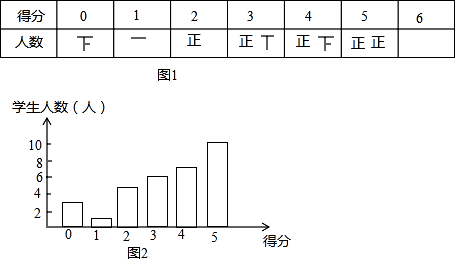
已知全班同学此题的平均得分为4分，结合表格解决下列问题：

（1）完成表格，并求该班学生总数；

（2）根据表中提供的数据，补全条形统计图；并判断下列说法中正确的有．（填序号即可）
①该班此题得分的众数是6；

②“随机抽取该班一份试卷，此题得1分”是不可能事件；

③该班学生此题得分的中位数是4；

④若将“该班同学本道题的得分情况”绘制成扇形统计图，求“此题得0分”的人数所对应的圆心角的度数为36°；

（3）若本年级学生共有540人，请你估计整个年级中此题得满分的学生人数．

查看解析收藏纠错

+选题
35.
一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52

78
88
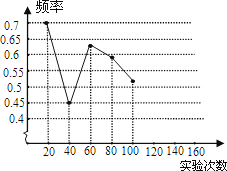
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56

（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？

查看解析收藏纠错

+选题
36. 某批乒乓球的质量检验结果如下：
抽取的乒乓球数n
200
500
1000
1500
2000
优等品频数m
188
471
946
1426
1898
优等品频率 $\text{[math]}$
0.940
0.942
0.946
0.951
0.949
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于 $\text{[math]}$ ，问至少取出了多少个黑球？

查看解析收藏纠错

+选题

四、综合题

37. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200km，210km，220km，230km，获得如下不完整的统计图。

根据以上信息，解答下列问题：

（1）这次被抽检的电动汽车共有多少辆？请补全条形统计图；

（2）估计这种电动汽车一次充电后行驶的平均里程数。

查看解析收藏纠错

+选题

38. 树叶有关的问题：

如图，一片树叶的长是指沿叶脉方向量出的最长部分的长度（不含叶柄）树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度，树叶的长宽比是指树叶的长与树叶的宽的比值．

某同学在校园内随机收集了 $\text{[math]}$ 树、 $\text{[math]}$ 树、 $\text{[math]}$ 树三棵的树叶各 $\text{[math]}$ 片，通过测量得到这些树叶的长 $\text{[math]}$ （单位： $\text{[math]}$ ），宽 $\text{[math]}$ （单位： $\text{[math]}$ ）的数据，计算长宽比，整理如下：

表1 $\text{[math]}$ 树、 $\text{[math]}$ 树、 $\text{[math]}$ 树树叶的长宽比统计表

	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

表2 $\text{[math]}$ 树、 $\text{[math]}$ 树、 $\text{[math]}$ 树树叶的长宽比的平均数、中位数、众数、方差统计表

	平均数	中位数	众数	方差
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$ 树树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

$\text{[math]}$ 树、 $\text{[math]}$ 树、 $\text{[math]}$ 树树叶的长随宽变化的情况（图1）

解决下列问题：

（1）写出表2中 $\text{[math]}$ ， $\text{[math]}$ 的值．

（2） ①小张同学说：“根据以上信息，我能判断 $\text{[math]}$ 树树叶的长、宽近似相等．”

②小李同学说：“从树叶的长宽比的平均数来看，我认为，下图的树叶是 $\text{[math]}$ 树的树叶．”

请你判断上面两位同学的说法中，谁的说法是合理的，谁的说法是不合理的，并给出你的理由．

（3）现有一片长 $\text{[math]}$ ，宽 $\text{[math]}$ 的树叶，请将该树叶的数用“★”表示在图1中，判断这片树叶更可能来自于 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中的哪棵树？并给出你的理由．

查看解析收藏纠错

+选题

抽查小麦粒数	100	300	800	1000	2000	3000
发芽粒数	96	287	770	958	1923	a

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的频率 $\text{[math]}$	0.58	0.64	0.58	0.59	0.605	0.601

实验次数	20	40	60	80	100	120	140	160
“車”字朝上的频数	14	18	38	47	52		78	88
相应的频率	0.7	0.45	0.63	0.59	0.52	0.55	0.56

抽取的乒乓球数n	200	500	1000	1500	2000
优等品频数m	188	471	946	1426	1898
优等品频率 $\text{[math]}$	0.940	0.942	0.946	0.951	0.949

2022年中考数学二轮专题复习-数据搜集整理数据分析概率

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨