2022年北师大数学七下期中复习阶梯训练：相交线与平行线（基础巩固）

1. 若 $\text{[math]}$ 的补角是 $\text{[math]}$ ，则 $\text{[math]}$ 的余角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图所示， $\text{[math]}$ 是平角， $\text{[math]}$ 是射线， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的角平分线，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 56° B . 62° C . 72° D . 124°

查看解析收藏纠错

+选题
3. 若∠A=40°，则∠A的补角为（）

A . 40° B . 50° C . 60° D . 140°

查看解析收藏纠错

+选题
4. 下面四个图形中，∠1与∠2是对顶角的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，河道的一侧有A、B两个村庄，现要铺设一条引水管道把河水引向A、B两村，下列四种方案中最节省材料的是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 一个角的度数等于 $\text{[math]}$ ，那么它的余角等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 下列说法错误的是（）

A . 等角的余角相等 B . 两点之间线段最短 C . 正数和0的绝对值等于它本身 D . 单项式 $\text{[math]}$ 的系数是 $\text{[math]}$ ，次数是2

查看解析收藏纠错

+选题
8. 下列说法错误的是（）

A . 连接两点的线段叫两点之间的距离 B . 经过两点有一条直线，并且只有一条直线 C . 两点的所有连线中，线段最短 D . 同角（等角）的补角相等

查看解析收藏纠错

+选题
9. 若∠A与∠B互为补角，且∠A＝28°，则∠B的度数是（）

A . 152° B . 28° C . 52° D . 90°

查看解析收藏纠错

+选题
10. 如图，点A在点O的南偏东20°方向上，且射线OA与OB 的夹角是110°，则射线OB的方向是（ )

A . 北偏东70° B . 北偏东60° C . 北偏东50° D . 北偏东40°

查看解析收藏纠错

+选题

11. 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的余角为．

查看解析收藏纠错

+选题
12. 已知一个角的度数为25°，则它的余角度数等于．

查看解析收藏纠错

+选题
13. 若一个角度数是115°6′，则这个角的补角是．

查看解析收藏纠错

+选题
14. $\text{[math]}$ 的余角等于．

查看解析收藏纠错

+选题
15. 已知∠AOC和∠BOD是一组对顶角，若∠AOC＝40°，则∠BOD＝．

查看解析收藏纠错

+选题
16. 已知∠A的补角是142°，则∠A的余角的度数是.

查看解析收藏纠错

+选题

17. 如图，直线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点O， $\text{[math]}$ 是 $\text{[math]}$ 平分线， $\text{[math]}$ ，求 $\text{[math]}$ 度数.

查看解析收藏纠错

+选题
18. 如图，直线AB与CD相交于点O，OE是∠COB的平分线，OE⊥OF，∠AOD=74°，求∠COF的度数．

查看解析收藏纠错

+选题
19. 已知：如图，AD∥BE，∠1＝∠2，求证：∠A＝∠E．

查看解析收藏纠错

+选题
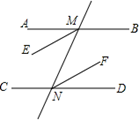
20. 如图，已知直线AB∥CD ，直线MN分别交AB、CD于M、N两点，若ME、NF分别是∠AMN、∠DNM的角平分线，试说明：ME∥NF
解：∵AB∥CD ，（ ▲ ）

∴∠AMN＝∠DNM（ ▲）

∵ME、NF分别是∠AMN、∠DNM的角平分线，（已知）

∴∠EMN＝ ▲∠AMN ，

∠FNM＝ ▲∠DNM （角平分线的定义）

∴∠EMN＝∠FNM（等量代换）

∴ME∥NF（ ▲）

由此我们可以得出一个结论：两条平行线被第三条直线所截，一对 ▲角的平分线互相 ▲ ．

查看解析收藏纠错

+选题
21. 如图是一个湖泊，C是湖泊外的一块田地，现欲挖一条水渠从湖泊AB将水引到C处．问：从湖泊AB的何处开挖，才能使所挖水渠最短？画图表示，并说明设计理由．

查看解析收藏纠错

+选题
22. 如图，∠1+∠2=180°。求证：a∥b。

查看解析收藏纠错

+选题

23. 如图，直线 $\text{[math]}$ 相交于点 $\text{[math]}$ 平分 $\text{[math]}$ ，求：

（1） $\text{[math]}$ 的度数.

（2） $\text{[math]}$ 的度数.

查看解析收藏纠错

+选题
24. 如图， AC平分∠MAE，交DB于点F.

（1）若AB∥CE，∠BAE=50°，求∠ACE的度数；

（2）若∠AFB=∠CAM，说明∠ACE=∠BDE的理由.

查看解析收藏纠错

+选题
25. 如图，已知直线AB和CD相交于点O，∠COE＝90°，OF平分∠AOE．

（1）写出∠BOE的余角；

（2）若∠COF的度数为29°，求∠BOE的度数．

查看解析收藏纠错

+选题

2022年北师大数学七下期中复习阶梯训练：相交线与平行线（基础巩固）

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

2022年北师大数学七下期中复习阶梯训练：相交线与平行线（基础巩固）

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨