17. 孔子雕像的落成给某中学增添了一处靓丽的人文景观,弘扬了优秀传统文化,也提升了学校的文化品位.学完了三角函数知识后,该校“数学社团”的张萍萍和杨霞同学决定用自己学到的知识测量孔子雕像的高度,她们把“测量孔子雕像的高”作为一项课题活动,并制定了测量方案,利用课余时间完成了实地测量,测量结果如表:
|
课题
|
测量孔子雕像的高
|
|
测量
示意图
|
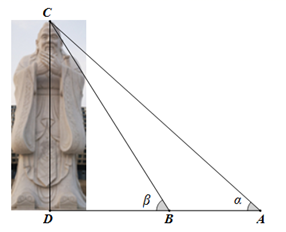 | 说明:在点  处测得孔子雕像顶端 处测得孔子雕像顶端  的仰角 的仰角  ,在点 ,在点  处测得孔子雕像顶端 处测得孔子雕像顶端  的仰角 的仰角  .( .(  , ,  , ,  三点在同一条直线上) 三点在同一条直线上) |
| 测量数据 |  的度数 的度数 |  的度数 的度数 |  的距离 的距离 |
|  |  |  |
请你根据他们测量的数据计算孔子雕像的高度.(结果精确到  .参考数据:
.参考数据:  ,
,  ,
,  )
)

≈1.73)