2022年苏科版初中数学《中考一轮复习》专题三函数 3.7 二次函数的动态几何问题

1. 如图，在△ABC中，∠C=90°，AB=10cm，BC=8cm，点P从点A沿AC向点C以1cm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止），在运动过程中，四边形PABQ的面积最小值为（）

A . 19cm² B . 16cm² C . 15cm² D . 12cm²

查看解析收藏纠错

+选题
2. 点C是线段AB上的一点，AB=1，分别以AC和CB为一边作正方形，用S表示这两个正方形的面积之和，下列判断正确的是（）

A . 当C是AB的中点时，S最小 B . 当C是AB的中点时，S最大 C . 当C为AB的三等分点时，S最小 D . 当C是AB的三等分点时，S最大

查看解析收藏纠错

+选题
3. 如图，抛物线与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿线段 $\text{[math]}$ 向点 $\text{[math]}$ 匀速运动，到达点 $\text{[math]}$ 停止， $\text{[math]}$ 轴，交抛物线于点 $\text{[math]}$ ．设点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ 秒．当 $\text{[math]}$ 和 $\text{[math]}$ 时， $\text{[math]}$ 的值相等．下列结论错误的是（）

A . $\text{[math]}$ 时， $\text{[math]}$ 的值最大 B . $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 和 $\text{[math]}$ 时， $\text{[math]}$ 的值不一定相等 D . $\text{[math]}$ 时， $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图1，在△ABC中，∠B＝90°，∠C＝30°，动点P从点B开始沿边BA、AC向点C以恒定的速度移动，动点Q从点B开始沿边BC向点C以恒定的速度移动，两点同时到达点C，设△BPQ的面积为y（cm²）.运动时间为x（s），y与x之间关系如图2所示，当点P恰好为AC的中点时，PQ的长为（）

A . 2 B . 4 C . 2 $\text{[math]}$ D . 4 $\text{[math]}$

查看解析收藏纠错

+选题
5. 已知抛物线y= $\text{[math]}$ x²+1具有如下性质：该抛物线上任意一点到定点F（0，2）的距离与到x轴的距离始终相等，如图，点M的坐标为（ $\text{[math]}$ ，3），P是抛物线y= $\text{[math]}$ x²+1上一个动点，则△PMF周长的最小值是（）

A . 4 B . 5 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒2个单位的速度沿折线 $\text{[math]}$ 运动到点 $\text{[math]}$ ，同时动点 $\text{[math]}$ 也从点 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 个单位的速度沿 $\text{[math]}$ 运动到点 $\text{[math]}$ ，当一个点停止运动时，另一个点也随之停止.设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，运动时间为 $\text{[math]}$ 秒，则下列图象能大致反映 $\text{[math]}$ 与 $\text{[math]}$ 之间函数关系的是（）

A . B . C . D .

查看解析收藏纠错

+选题
7. 如图，矩形OABC的顶点A、C分别在x轴、y轴上，OA＝4，OC＝3，直线m：y＝﹣ $\text{[math]}$ x从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M ， N ，直线m运动的时间为t(秒)，设△OMN的面积为S ，则能反映S与t之间函数关系的大致图象是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图，直线 $\text{[math]}$ 与x轴和y轴分别相交于A、B两点，平行于直线 $\text{[math]}$ 的直线 $\text{[math]}$ 从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴和y轴分别相交于C、D两点，运动时间为t秒 $\text{[math]}$ .以 $\text{[math]}$ 为斜边作等腰直角 $\text{[math]}$ （E、O两点分别在 $\text{[math]}$ 两侧），若 $\text{[math]}$ 和 $\text{[math]}$ 的重合部分的面积为S，则S与t之间的函数关系的图象大致是（）

A . B . C . D .

查看解析收藏纠错

+选题
9. 如图，边长为2的正△ABC的边BC在直线l上，两条距离为l的平行直线a和b垂直于直线l，a和b同时向右移动（a的起始位置在B点），速度均为每秒1个单位，运动时间为t（秒），直到b到达C点停止，在a和b向右移动的过程中，记△ABC夹在a和b之间的部分的面积为s，则s关于t的函数图象大致为（）

A . B . C . D .

查看解析收藏纠错

+选题
10. 如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P与点B、C都不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（　　）

A . B . C . D .

查看解析收藏纠错

+选题

11. 如图，在Rt△ABC中，∠BAC=90°，AB=AC=16cm ， AD为BC边上的高，动点P从点A出发，沿A→D方向以 $\text{[math]}$ cm/s的速度向点D运动，过P点作PE∥BC交AC于点E ，过E点作EF⊥BC于点F ，设△ABP的面积为S₁ ，四边形PDFE的面积为S₂ ，则点P在运动过程中，S₁+S₂的最大值为．

查看解析收藏纠错

+选题
12. 如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过秒，四边形APQC的面积最小．

查看解析收藏纠错

+选题
13. 如图，已知二次函数 $\text{[math]}$ 的图象交x轴于A(－1，0)，B(4，0)，交y轴于点C，点P是直线BC上方抛物线上一动点（不与B，C重合），过点P作PE⊥BC，PF∥y轴交BC与F，则△PEF面积的最大值是.

查看解析收藏纠错

+选题
14. 如图，已知直线y=﹣ $\text{[math]}$ x+3分别交x轴、y轴于点A、B，P是抛物线y=﹣ $\text{[math]}$ x²+2x+5上的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=﹣ $\text{[math]}$ x+3于点Q，则当PQ=BQ时，a的值是．

查看解析收藏纠错

+选题
15. 如图，已知⊙P的半径为2，圆心P在抛物线y= $\text{[math]}$ ﹣1上运动，当⊙P与x轴相切时，圆心P的坐标为．

查看解析收藏纠错

+选题
16. 如图，已知直线y=- $\text{[math]}$ x+3分别交x轴、y轴于点A、B，P是抛物线y=- $\text{[math]}$ x²+2x+5的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=- $\text{[math]}$ x+3于点Q，则当PQ=BQ时，a的值是．

查看解析收藏纠错

+选题
17. 如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为 s时，四边形EFGH的面积最小，其最小值是 cm² ．

查看解析收藏纠错

+选题
18. 如图，二次函数 $\text{[math]}$ 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C ，其对称轴与x轴交于点D ，若P为y轴上的一个动点，连接PD ，则 $\text{[math]}$ PC+PD的最小值为．

查看解析收藏纠错

+选题

19. 如图所示，在矩形ABCD中，AB=6厘米，BC=12厘米，点P在线段AB上，P从点A开始沿AB边以1厘米/秒的速度向点B移动．点E为线段BC的中点，点Q从E点开始，沿EC以1厘米/秒的速度向点C移动．如果P、Q同时分别从A、E出发，写出出发时间t与△BPQ的面积S的函数关系式，求出t的取值范围．

查看解析收藏纠错

+选题
20. 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于C点， $\text{[math]}$ ， $\text{[math]}$ .

（1）求抛物线的解析式；

（2）在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大.求出点P的坐标

（3）在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q.使点P、B、M、Q为顶点的四边形是平行四边形，若存在.请直接写出Q点的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
21.
如图，一条抛物线经过原点和点C（8，0），A、B是该抛物线上的两点，AB∥x轴，OA=5，AB=2．点E在线段OC上，作∠MEN=∠AOC，使∠MEN的一边始终经过点A，另一边交线段BC于点F，连接AF．

（1）求抛物线的解析式；
（2）当点F是BC的中点时，求点E的坐标；
（3）当△AEF是等腰三角形时，求点E的坐标．

查看解析收藏纠错

+选题
22.
在平面直角坐标系xOy中，抛物线的解析式是y＝ $\text{[math]}$ x²＋1，点C的坐标为（－4，0），平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q（x，y）在抛物线上，点P（t，0）在x轴上.

（1）写出点M的坐标；
（2）当四边形CMQP是以MQ，PC为腰的梯形时；
①求t关于x的函数解析式和自变量x的取值范围；
②当梯形CMQP的两底的长度之比为1∶2时，求t的值.

查看解析收藏纠错

+选题
23.
如图，抛物线 $\text{[math]}$ 与x轴交于A、C两点，与y轴交于B点．

（1）求△AOB的外接圆的面积；
（2）若动点P从点A出发，以每秒1个单位沿射线AC方向运动；同时，点Q从点B出发，以每秒0.5个单位沿射线BA方向运动，当点P到达点C处时，两点同时停止运动．问当t为何值时，以A、P、Q为顶点的三角形与△OAB相似？
（3）若M为线段AB上一个动点，过点M作MN平行于y轴交抛物线于点N．
问：是否存在这样的点M，使得四边形OMNB恰为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
24. 如图，抛物线y= $\text{[math]}$ x²+mx+n与直线y=﹣ $\text{[math]}$ x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）.

（1）求抛物线的解析式和tan∠BAC的值；

（2）在（1）条件下：
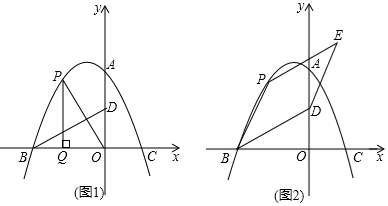
（Ⅰ）P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由.

（Ⅱ）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位速度运动到E点，再沿线段EA以每秒 $\text{[math]}$ 个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？

查看解析收藏纠错

+选题
25. 如图，在平面直角坐标系中，二次函数y＝﹣ $\text{[math]}$ x²+bx+c的图象与y轴交于点A（0，8），与x轴交于B、C两点，其中点C的坐标为（4，0）.点P（m，n）为该二次函数在第二象限内图象上的动点，点D的坐标为（0，4），连接BD.

（1）求该二次函数的表达式及点B的坐标；

（2）连接OP，过点P作PQ⊥x轴于点Q，当以O、P、Q为顶点的三角形与△OBD相似时，求m的值；

（3）连接BP，以BD、BP为邻边作▱BDEP，直线PE交y轴于点T.
①当点E落在该二次函数图象上时，求点E的坐标；

②在点P从点A到点B运动过程中（点P与点A不重合），直接写出点T运动的路径长.

查看解析收藏纠错

+选题
26. 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．连结 $\text{[math]}$ ，以 $\text{[math]}$ 为一边，点 $\text{[math]}$ 为对称中心作菱形 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 轴上的一个动点，设点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线 $\text{[math]}$ 交抛物线于点 $\text{[math]}$ ．

（1）求点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的坐标；

（2）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动时，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ ．试探究 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 是平行四边形；

（3）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动时，是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 为直角三角形，若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
27. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C，点P是第一象限内抛物线上的动点.

（1）求抛物线的解析式；

（2）连接BC与OP，交于点D，求当 $\text{[math]}$ 的值最大时点P的坐标；

（3）点F与点C关于抛物线的对称轴成轴对称，当点P的纵坐标为2时，过点P作直线PQ∥x轴，点M为直线PQ上的一个动点，过点M作MN⊥x轴于点N，在线段ON上任取一点K，当有且只有一个点K满足∠FKM＝135°时，请直接写出此时线段ON的长.

查看解析收藏纠错

+选题
28. 如图1，抛物与 y=ax²+bx+4（a＜0）与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点C

（1）求该抛物线对应的函数表达式，并写出其顶点M的坐标

（2）试在y轴上找一点T，使得TM⊥TB，求T点的坐标

（3）如图2，连接BC，点D是直线BC上方抛物线上的点，连接OD、CD，OD交BC于点F，当 $\text{[math]}$ 时，求点D的坐标

（4）如图3，点E的坐标为（0，-2），点P是抛物线上的动点，连接EB，PB，PE形成的△PBE中，是否存在点P，使得∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的P点坐标；若不存在，请说明理由

查看解析收藏纠错

+选题

2022年苏科版初中数学《中考一轮复习》专题三函数 3.7 二次函数的动态几何问题

一、单选题

二、填空题

三、解答题

相关试卷收起∨

2022年苏科版初中数学《中考一轮复习》专题三 函数 3.7 二次函数的动态几何问题

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

2022年苏科版初中数学《中考一轮复习》专题三函数 3.7 二次函数的动态几何问题

相关试卷收起∨