天津市中考数学真题汇编（近五年） 3 函数

1. 若点A（﹣1，y₁），B（1，y₂），C（3，y₃）在反比例函数 $\text{[math]}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A . y₁＜y₂＜y₃ B . y₂＜y₃＜y₁ C . y₃＜y₂＜y₁ D . y₂＜y₁＜y₃

查看解析收藏纠错

+选题
2. 已知抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ）经过点 $\text{[math]}$ ，当 $\text{[math]}$ 时，与其对应的函数值 $\text{[math]}$ ．有下列结论：① $\text{[math]}$ ；②关于x的方程 $\text{[math]}$ 有两个不等的实数根；③ $\text{[math]}$ ．其中，正确结论的个数是（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
3. 若点 $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图，四边形 $\text{[math]}$ 是正方形，O ， D两点的坐标分别是 $\text{[math]}$ ， $\text{[math]}$ ，点C在第一象限，则点C的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 若点 $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图像上，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 已知二次函数y=（x﹣h）²+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）

A . 1或﹣5 B . ﹣1或5 C . 1或﹣3 D . 1或3

查看解析收藏纠错

+选题
8. 若点A（﹣5，y₁），B（﹣3，y₂），C（2，y₃）在反比例函数y= $\text{[math]}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A . y₁＜y₃＜y₂ B . y₁＜y₂＜y₃ C . y₃＜y₂＜y₁ D . y₂＜y₁＜y₃

查看解析收藏纠错

+选题
9. 已知抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为常数， $\text{[math]}$ ）经过点 $\text{[math]}$ . ， $\text{[math]}$ ，其对称轴在 $\text{[math]}$ 轴右侧，有下列结论：①抛物线经过点 $\text{[math]}$ ；②方程 $\text{[math]}$ 有两个不相等的实数根；③ $\text{[math]}$ .，正确结论的个数为（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
10. 二次函数y＝ax²+bx+c（a ， b ， c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：

x

…

﹣2

﹣1

0

1

2

…

y＝ax²+bx+c

…

t

m

﹣2

﹣2

n

…

且当x＝﹣ $\text{[math]}$ 时，与其对应的函数值y＞0．有下列结论：

①abc＞0；②﹣2和3是关于x的方程ax²+bx+c＝t的两个根；③0＜m+n＜ $\text{[math]}$ ．

其中，符合题意结论的个数是（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
11. 已知抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ）经过点 $\text{[math]}$ ，其对称轴是直线 $\text{[math]}$ ．有下列结论：
① $\text{[math]}$ ；②关于x的方程 $\text{[math]}$ 有两个不等的实数根；③ $\text{[math]}$ ．其中，正确结论的个数是（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
12. 已知抛物线y=x²﹣4x+3与x轴相交于点A，B（点A在点B左侧），顶点为M．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（）

A . y=x²+2x+1 B . y=x²+2x﹣1 C . y=x²﹣2x+1 D . y=x²﹣2x﹣1

查看解析收藏纠错

+选题
13.
如图，在直角坐标系xOy中，点A，B分别在x轴和y轴， $\text{[math]}$ ． ∠AOB的角平分线与OA的垂直平分线交于点C，与AB交于点D，反比例函数y= $\text{[math]}$ 的图象过点C．当以CD为边的正方形的面积为 $\text{[math]}$ 时，k的值是（　　）

A . 2 B . 3 C . 5 D . 7

查看解析收藏纠错

+选题

14. 将直线 $\text{[math]}$ 向下平移2个单位长度，平移后直线的解析式为．

查看解析收藏纠错

+选题
15. 直线y＝2x﹣1与x轴的交点坐标为．

查看解析收藏纠错

+选题
16. 将直线 $\text{[math]}$ 向上平移2个单位长度，平移后直线的解析式为．

查看解析收藏纠错

+选题
17. 若正比例函数y=kx（k是常数，k≠0）的图象经过第二、四象限，则k的值可以是（写出一个即可）．

查看解析收藏纠错

+选题
18. 将直线 $\text{[math]}$ 向上平移1个单位长度，平移后直线的解析式为．

查看解析收藏纠错

+选题
19. 若一次函数y=﹣2x+b（b为常数）的图象经过第二、三、四象限，则b的值可以是（写出一个即可）．

查看解析收藏纠错

+选题

20. 已知抛物线 $\text{[math]}$ （a，c为常数， $\text{[math]}$ ）经过点 $\text{[math]}$ ，顶点为D．
（Ⅰ）当 $\text{[math]}$ 时，求该抛物线的顶点坐标；

（Ⅱ）当 $\text{[math]}$ 时，点 $\text{[math]}$ ，若 $\text{[math]}$ ，求该抛物线的解析式；

（Ⅲ）当 $\text{[math]}$ 时，点 $\text{[math]}$ ，过点C作直线l平行于x轴， $\text{[math]}$ 是x轴上的动点， $\text{[math]}$ 是直线l上的动点．当a为何值时， $\text{[math]}$ 的最小值为 $\text{[math]}$ ，并求此时点M，N的坐标．

查看解析收藏纠错

+选题
21. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

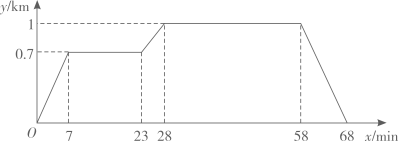
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍 $\text{[math]}$ ，图书馆离宿舍 $\text{[math]}$ ．周末，小亮从宿舍出发，匀速走了 $\text{[math]}$ 到食堂；在食堂停留 $\text{[math]}$ 吃早餐后，匀速走了 $\text{[math]}$ 到图书馆；在图书馆停留 $\text{[math]}$ 借书后，匀速走了 $\text{[math]}$ 返回宿舍，给出的图象反映了这个过程中小亮离宿舍的距离 $\text{[math]}$ 与离开宿舍的时间 $\text{[math]}$ 之间的对应关系．

请根据相关信息，解答下列问题：

（1）填表：

离开宿舍的时间/ $\text{[math]}$

2

5

20

23

30

离宿舍的距离/ $\text{[math]}$

0.2

0.7

（2）填空：
①食堂到图书馆的距离为 $\text{[math]}$ ．

②小亮从食堂到图书馆的速度为 $\text{[math]}$ ．

③小亮从图书馆返回宿舍的速度为 $\text{[math]}$ ．

④当小亮离宿舍的距离为 $\text{[math]}$ 时，他离开宿舍的时间为 $\text{[math]}$ ．

（3）当 $\text{[math]}$ 时，请直接写出y关于x的函数解析式．

查看解析收藏纠错

+选题
22. 在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D ， E ， C分别在OA ， AB ， OB上，OD＝2．

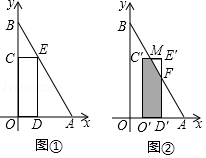
（Ⅰ）如图①，求点E的坐标；

（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C ， O ， D ， E的对应点分别为C′，O′，D′，E′．设OO′＝t ，矩形C′O′D′E′与△ABO重叠部分的面积为S ．

①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M ， F ，试用含有t的式子表示S ，并直接写出t的取值范围；

②当 $\text{[math]}$ ≤S≤5 $\text{[math]}$ 时，求t的取值范围（直接写出结果即可）．

查看解析收藏纠错

+选题
23. 已知二次函数y=x²+bx+c（b ， c为常数）．
（Ⅰ）当b=2，c=﹣3时，求二次函数的最小值；

（Ⅱ）当c=5时，若在函数值y=l的怙况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；

（Ⅲ）当c=b²时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．

查看解析收藏纠错

+选题

24. 在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ .已知抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数），顶点为 $\text{[math]}$ .

（1）当抛物线经过点 $\text{[math]}$ 时，求顶点 $\text{[math]}$ 的坐标；

（2）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴下方，当 $\text{[math]}$ 时，求抛物线的解析式；

（3）无论 $\text{[math]}$ 取何值，该抛物线都经过定点 $\text{[math]}$ .当 $\text{[math]}$ 时，求抛物线的解析式.

查看解析收藏纠错

+选题
25. 某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.
设小明计划今年夏季游泳次数为 $\text{[math]}$ （ $\text{[math]}$ 为正整数）.

（1）根据题意，填写下表：
游泳次数
10
15
20
…
$\text{[math]}$
方式一的总费用（元）
150
175
…
方式二的总费用（元）
90
135
…

（2）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？

（3）当 $\text{[math]}$ 时，小明选择哪种付费方式更合算？并说明理由.

查看解析收藏纠错

+选题
26. 已知抛物线y=x²+bx﹣3（b是常数）经过点A（﹣1，0）．

（1）求该抛物线的解析式和顶点坐标；

（2） P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．
①当点P'落在该抛物线上时，求m的值；
②当点P'落在第二象限内，P'A²取得最小值时，求m的值．

查看解析收藏纠错

+选题
27. 公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元

（1）设租用甲种货车x辆（x为非负整数），试填写表格．
表一：
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二：
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2800
租用乙种货车的费用/元
280

（2）给出能完成此项运送任务的最节省费用的租车方案，并说明理由．

查看解析收藏纠错

+选题
28. 已知点 $\text{[math]}$ 是抛物线 $\text{[math]}$ （ $\text{[math]}$ 为常数， $\text{[math]}$ ）与x轴的一个交点．

（1）当 $\text{[math]}$ 时，求该抛物线的顶点坐标；

（2）若抛物线与x轴的另一个交点为 $\text{[math]}$ ，与y轴的交点为C ，过点C作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点， $\text{[math]}$ ．
①当点E落在抛物线上（不与点C重合），且 $\text{[math]}$ 时，求点F的坐标；

②取 $\text{[math]}$ 的中点N ，当m为何值时， $\text{[math]}$ 的最小值是 $\text{[math]}$ ？

查看解析收藏纠错

+选题
29. 用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．
设在同一家复印店一次复印文件的页数为x（x为非负整数）．

（1）根据题意，填写下表：
一次复印页数（页）
5
10
20
30
…
甲复印店收费（元）
0.5
2
…
乙复印店收费（元）
0.6
2.4
…

（2）设在甲复印店复印收费y₁元，在乙复印店复印收费y₂元，分别写出y₁ ， y₂关于x的函数关系式；

（3）当x＞70时，顾客在哪家复印店复印花费少？请说明理由．

查看解析收藏纠错

+选题

30. 甲、乙两个批发店销售同一种苹果，在甲批发店，不论一次购买数量是多少，价格均为6元/kg ．在乙批发店，一次购买数量不超过50kg时，价格为7元/kg；一次购买数量超过50kg时，其中有50kg的价格仍为7元/kg ，超过50kg部分的价格为5元/kg ．设小王在同一个批发店一次购买苹果的数量为xkg（x＞0）．

（1）根据题意填表：

一次购买数量/kg	30	50	150	…
甲批发店花费/元		300		…
乙批发店花费/元		350		…

（2）设在甲批发店花费y₁元，在乙批发店花费y₂元，分别求y₁ ， y₂关于x的函数解析式；

（3）根据题意填空：

①若小王在甲批发店和在乙批发店一次购买苹果的数量相同，且花费相同，则他在同一个批发店一次购买苹果的数量为kg；

②若小王在同一个批发店一次购买苹果的数量为120kg ，则他在甲、乙两个批发店中的批发店购买花费少；

③若小王在同一个批发店一次购买苹果花费了360元，则他在甲、乙两个批发店中的批发店购买数量多．

查看解析收藏纠错

+选题

31. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

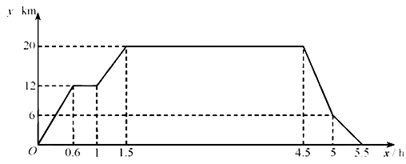
已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $\text{[math]}$ ，陈列馆离学校 $\text{[math]}$ ．李华从学校出发，匀速骑行 $\text{[math]}$ 到达书店；在书店停留 $\text{[math]}$ 后，匀速骑行 $\text{[math]}$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $\text{[math]}$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $\text{[math]}$ 与离开学校的时间 $\text{[math]}$ 之间的对应关系．

请根据相关信息，解答下列问题：

（1）填表

离开学校的时间/ $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

离学校的距离/ $\text{[math]}$

2

12

（2）填空：
①书店到陈列馆的距离为 $\text{[math]}$ ；

②李华在陈列馆参观学的时间为h；

③李华从陈列馆回学校途中，减速前的骑行速度为 $\text{[math]}$ ；

④当李华离学校的距离为 $\text{[math]}$ 时，他离开学校的时间为h．

（3）当 $\text{[math]}$ 时，请直接写出y关于x的函数解析式．

查看解析收藏纠错

+选题

天津市中考数学真题汇编（近五年） 3 函数

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

离开宿舍的时间/ $\text{[math]}$	2	5	20	23	30
离宿舍的距离/ $\text{[math]}$	0.2		0.7

游泳次数	10	15	20	…	$\text{[math]}$
方式一的总费用（元）	150	175		…
方式二的总费用（元）	90	135		…

租用甲种货车的数量/辆	3	7	x
租用的甲种货车最多运送机器的数量/台	135
租用的乙种货车最多运送机器的数量/台	150

租用甲种货车的数量/辆	3	7	x
租用甲种货车的费用/元		2800
租用乙种货车的费用/元		280

一次复印页数（页）	5	10	20	30	…
甲复印店收费（元）	0.5		2		…
乙复印店收费（元）	0.6		2.4		…

离开学校的时间/ $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
离学校的距离/ $\text{[math]}$	2			12

x	…	﹣2	﹣1	0	1	2	…
y＝ax²+bx+c	…	t	m	﹣2	﹣2	n	…

天津市中考数学真题汇编（近五年） 3 函数

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨