修改时间:2024-07-13 浏览次数:254 类型:中考模拟
平均每天运动时间频数分布统计表
|
组别 |
时间t/小时 |
频数/人数 |
|
A |
| 10 |
| B | | 20 |
| C | | |
| D | | n |
平均每天运动时间扇形统计图

B组时间与人数分布表
| 时间(小时) | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 人数(人) | 1 | 2 | 4 | 6 | 7 |
根据以上信息解答问题.
|
仅用圆规三等分.六等分圆是容易的,而四等分、五等分…则有一定难度,历史上卡尔·弗雷德里希·高斯首次解决了将圆十七等分的难题.拿破仑·波拿巴当年曾向数学家提出这样一个问题:只用圆规,不用直尺,如何把一个圆周四等分?这个难题最终由意大利数学家马斯凯罗尼解决了.为此,他还写了名为《圆规几何》的书献给拿破仑,书中还包含了更深刻的作图理论.他给出的作图步骤和部分证明如下: 如图1, 第一步:在⊙O上任取一点A,以点A为一个分点,将⊙O六等分,其他分点依次为B、C、D、E、F; 第二步:分别以A、D两点为圆心,以 第三步:以点A为圆心, 则点A、M、D、N是⊙O的四等分点. 证明:如图2, 连接 ∵点A、B、C、D、E、F是⊙O的六等分点. |
任务:
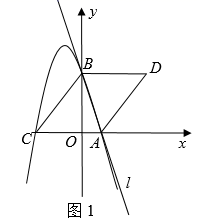
如图1,直线 :
与x轴,y轴分别交于A,B两点,抛物线
经过A,B两点,与x轴的另一个交点为点C,连接
,作
关于直线l对称的
.
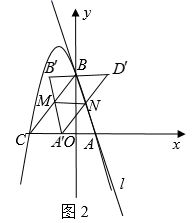
①求S与t的函数关系式;
②当 轴时,求S的值;
试题篮