修改时间:2021-05-31 浏览次数:173 类型:中考模拟
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
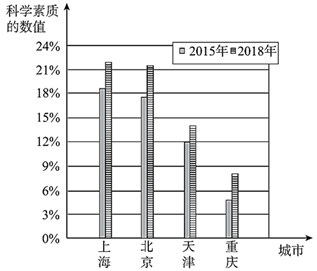
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
| 2015年 | 2018年 | |
| 男 | | |
| 女 | | |
c.2001年以来我国公民科学素质水平发展统计图如下:
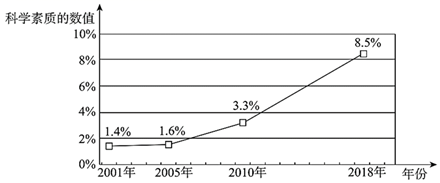
根据以上信息,回答下列问题:
已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
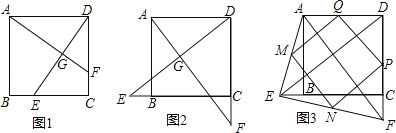
试题篮