浙教版备考2021年中考数学三轮冲刺复习专题6 四边形

1. 如果一个正多边形内角和等于1080°，那么这个正多边形的每一个外角等于（）

A . 45° B . 60° C . 120° D . 135°

查看解析收藏纠错

+选题
2. 如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD＝12，AD：AB＝1：2，则图中阴影部分的面积为（）

A . 12 $\text{[math]}$ B . 15 $\text{[math]}$ -6π C . 30 $\text{[math]}$ ﹣12π D . $\text{[math]}$ π

查看解析收藏纠错

+选题
3. 我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，其中O点是坐标原点，AO＝2，BO＝3，BC＝4，点A、B是固定点，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A . 当AB=BC时，它是菱形 B . 当AC=BD时，它是正方形 C . 当AC⊥BD时，它是菱形 D . 当∠ABC=90°时，它是矩形

查看解析收藏纠错

+选题
5. 如图，在菱形OABC中，AC＝6，OB＝8，点O为原点，点B在y轴正半轴上，若函数y＝ $\text{[math]}$ （k≠0）的图象经过点C，则k的值是（）

A . 24 B . 12 C . ﹣12 D . ﹣6

查看解析收藏纠错

+选题
6. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC'D'，若∠D'AB=30°，则菱形ABC'D'的面积与正方形ABCD的面积之比是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）

A . 2 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，Rt△ACB中，∠C=90°，AC=6，BC=8，半径为1的⊙O与AC，BC相切，当⊙O沿边CB平移至与AB相切时，则⊙O平移的距离为（）

A . 3 B . 4 C . 5 D . 6

查看解析收藏纠错

+选题
9. 如图，在平面直角坐标系中，一个含有45〫角的三角板的其中一个锐角顶点置于点A（﹣3，﹣3）处，将其绕点A旋转，这个45〫角的两边所在的直线分别交x轴，y轴的正半轴于点B，C，连结BC，函数y＝ $\text{[math]}$ （x＞0）的图象经过BC的中点D，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，在矩形ABCD中，点E，F将对角线AC三等分，已知 AB＝9，BC＝12，点P在矩形ABCD的边上，则满足PE+PF＝12的点P的个数是（）

A . 2 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题

11. 如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为.

查看解析收藏纠错

+选题
12. 如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC、AD的中点，AF∥BC交CE的延长线于F，则△AFC的面积为.

查看解析收藏纠错

+选题
13. 如图，将边长为9的正方形纸片ABCD沿MN折叠，使点A落在BC边上 $\text{[math]}$ 点处，点D的对应点为点 $\text{[math]}$ ，若 $\text{[math]}$ ，则DM=.

查看解析收藏纠错

+选题
14. 已知E，F，G，H分别是四边形ABCD各边的中点，则当ACBD时，四边形EFGH是矩形．

查看解析收藏纠错

+选题
15. 如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连接BD并延长交EG于点T，交FG于点P，则GT＝.

查看解析收藏纠错

+选题
16. 在▱ABCD中，E是AD上一点，且点E将AD分为2：3的两部分，连接BE、AC相交于F，则S_△AEF：S_△CBF是.

查看解析收藏纠错

+选题
17. 如图2，小靓用边长为16的七巧板（如图1）拼成一幅装饰图，放入长方形ABCD内拼成一个“木马”形状（如图2），图中的三角形顶点E在边CD上，三角形的边AM、GF分别在边AD、BC上，则AB的长是.

查看解析收藏纠错

+选题
18. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，连结 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分六边形 $\text{[math]}$ 的周长为

查看解析收藏纠错

+选题

19. 如图，在平面直角坐标系xOy中，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点D、E、F、G分别为边OA、AB、BC、CO的中点，连结DE、EF、FG、GD.

（1）若点C在y轴的正半轴上，当点B的坐标为（2，4）时，判断四边形DEFG的形状，并说明理由.

（2）若点C在第二象限运动，且四边形DEFG为菱形时，求点四边形OABC对角线OB长度的取值范围.

（3）若在点C的运动过程中，四边形DEFG始终为正方形，当点C从X轴负半轴经过Y轴正半轴，运动至X轴正半轴时，直接写出点B的运动路径长.

查看解析收藏纠错

+选题
20. 已知：如图，四边形ABCD中，AD∥BC，对角线BD平分∠ABC，且BD⊥DC，E为BC中点，AB＝DE.

（1）求证：四边形ABED是菱形；

（2）若∠C＝60°，CD＝4，求四边形ABCD的面积.

查看解析收藏纠错

+选题
21. 如图1，若O是AB的中点，也是CD的中点，那么点称为AB与CD的结点。

（1）如图2，已知四边形ABCD的对角线交于点O，且O是AC，BD的结点，请直接写出满足要求的四边形ABCD的名称（写出两个即可）

（2）如图3，在Rt△ABC中，∠C=90°，O是AB的中点，E是BC上一点，G是AC上一点，连结EG，过点G作EG的垂线，交EO的延长线于点∠EGC=∠GDA。求证：O是AB，DE的结点。

（3）在（2）的条件下，当BC=8，AC=6 $\text{[math]}$ ，且EG=DO时，求DG的长。

查看解析收藏纠错

+选题
22. 如图，正方形OABC的顶点O与原点重合，点A，C分别在x轴与y轴的正半轴上，点A的坐标为（4，0），点D在边AB上，且tan∠AOD＝ $\text{[math]}$ ，点E是射线OB上一动点，EF⊥x轴于点F，交射线OD于点G，过点G作GH∥x轴交AE于点H.

（1）求B，D两点的坐标；

（2）当点E在线段OB上运动时，求∠HDA的大小；

（3）以点G为圆心，GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切？若不存在，请说明理由；若存在，请求出所有符合条件的点E的坐标.

查看解析收藏纠错

+选题
23. 如图，矩形ABCD中，AB=6，BC=6 $\text{[math]}$ ，动点P从点A出发，以每秒 $\text{[math]}$ 个单位长度的速度沿线段AD运动，动点Q从点D出发，以每秒2个单位长度的速度沿折线段D﹣O﹣C运动，已知P、Q同时开始移动，当动点P到达D点时，P、Q同时停止运动.设运动时间为t秒.

（1）当t=1秒时，求动点P、Q之间的距离；

（2）若动点P、Q之间的距离为4个单位长度，求t的值；

（3）若线段PQ的中点为M，在整个运动过程中；直接写出点M运动路径的长度.

查看解析收藏纠错

+选题
24. 如图

（1）方法体验：
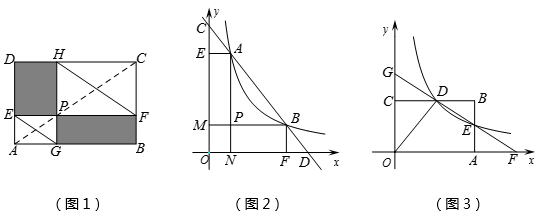
如图1，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H，容易证明四边形PEDH和四边形PFBG是面积相等的矩形，分别连结EG，FH.

①根据矩形PEDH和矩形PFBG面积相等的关系，那么PE·PH= ▲ .

②求证：EG∥FH.

（2）方法迁移：
如图2，已知直线 $\text{[math]}$ 分别与x轴，y轴交于D，C两点，

与双曲线 $\text{[math]}$ 交于A，B两点. 求证：AC=BD.

（3）知识应用：
如图3，反比例函数 $\text{[math]}$ （x＞0）的图象与矩形ABCO的边BC交于点D，与边AB交于点E，直线DE与x轴，y轴分别交于点F，G . 若矩形ABCO的面积为10，△ODG与△ODF的面积比为3：5，则k=.

查看解析收藏纠错

+选题
25. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .动点P以每秒5个单位长度的速度从点A出发，沿 $\text{[math]}$ 的方向向终点C运动.点P关于点C的对称点为D，过点P作 $\text{[math]}$ 于点Q，以 $\text{[math]}$ 、 $\text{[math]}$ 为边作 $\text{[math]}$ ，设点P的运动时间为 $\text{[math]}$ .

（1）当点P在 $\text{[math]}$ 上运动时，用含t的代数式表示 $\text{[math]}$ 的长.

（2）当 $\text{[math]}$ 为菱形时，求t的值.

（3）设 $\text{[math]}$ 的面积为S，求S与t之间的函数关系式.

（4）作点E关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 内部时，直接写出t的取值范围.

查看解析收藏纠错

+选题
26. 我们定义：连结凸四边形一组对边中点的线段叫做四边形的“准中位线”.

（1）概念理解：
如图1，四边形ABCD中，F为CD的中点，∠ADB=90°，E是AB边上一点，满足DE=AE，试判断EF是否为四边形ABCD的准中位线，并说明理由。

（2）问题探究：
如图2，△ABC中，∠ACB=90°，AC=6，BC=8，动点E以每秒1个单位的速度，从点A出发向点C运动，动点F以每秒6个单位的速度，从点C出发沿射线CB运动，当点E运动至点C时，两点同时停止运动。D为线段AB上任意一点，连接并延长CD，射线CD与点A，B，E，F构成的四边形的两边分别相交于点M，N，设运动时间为t。问t为何值时，MN为点A，B，E，F构成的四边形的准中位线。

（3）应用拓展：
如图3，EF为四边形ABCD的准中位线，AB=CD，延长FE分别与BA，CD的延长线交于点M，N，请找出图中与∠M相等的角并证明。

查看解析收藏纠错

+选题

浙教版备考2021年中考数学三轮冲刺复习专题6 四边形

一、单选题

二、填空题

三、综合题

相关试卷收起∨

浙教版备考2021年中考数学三轮冲刺复习专题6 四边形

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨