江西省九江三中、东湖中学2020年中考数学3月模拟试卷

修改时间：2024-07-31 浏览次数：180 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 下列四个数中，最大的数是（）

A . ﹣2 B . ﹣1 C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 据国家统计局公布的数据，2017年中国经济增速为6.9%，经济总量约为830000亿元，首次突破80万亿元．将830000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列共享单车的四个图标中，是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图①是一个正四棱锥，切去上面小的正四棱锥后得到一个正四棱台（上、下底均为正方形），如图②所示，则图②的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 下列计算错误的是(　　)

A . $\text{[math]}$ (ab≠0 ) B . ab²÷ $\text{[math]}$ =2ab³(b≠0) C . 2a²b+3ab²＝5a³b³ D . (ab²)³＝a³b⁶

查看解析收藏纠错

+选题
6. 如图，已知 $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若将 $\text{[math]}$ 先沿y轴进行第一次对称变换，所得图形沿x轴进行第二次对称变换，轴对称变换的对称轴遵循y轴、x轴、y轴、x轴…的规律进行，则经过第2018次变换后， $\text{[math]}$ 顶点A坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

7. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
8. 若方程2x²﹣4x﹣3＝0的两个实数根分别为出x₁ ， x₂ ，则x₁+x₂＝．

查看解析收藏纠错

+选题
9. 如图，O是直线AB上一点，∠AOC＝35°，CO⊥DO ， OC＝OB ， OD交CB于点E ，则∠CED＝．

查看解析收藏纠错

+选题
10. 点 $\text{[math]}$ ， $\text{[math]}$ 是反比例函数 $\text{[math]}$ $\text{[math]}$ 图象上两点，当 $\text{[math]}$ 时， $\text{[math]}$ ，那么一次函数 $\text{[math]}$ 的图象不经过第象限．

查看解析收藏纠错

+选题
11. “南昌之星”摩天轮，位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园，摩天轮高160m（最高点到地面的距离）．如图，点O是摩天轮的圆心，AB是其垂直于地面的直径，小贤在地面点C处利用测角仪测得摩天轮的最高点A的仰角为45°，测得圆心O的仰角为30°，则摩天轮的半径为m ．（结果保留根号）

查看解析收藏纠错

+选题
12. 已知二次函数C：y＝（x﹣2）²﹣2（0≤x≤3），点P在二次函数C的图象上，点A为x轴正半轴上一点，若tan∠AOP＝1，则点P的坐标为．

查看解析收藏纠错

+选题

三、解答题

13.

（1）计算： $\text{[math]}$

（2）如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
14. 解不等式组 $\text{[math]}$ 并在数轴上画出不等式组的解集．

查看解析收藏纠错

+选题
15. 小明从家到学校需要中途转车，从家到站台P有A、B、C三路车（乘A、B、C三路车的可能性相同）．到了站台P后转乘D路或E路到学校（乘D路、E路车的可能性相同）．

（1） “小明从家到学校乘A路车”是事件；

（2）请用列表或画树状图的方法，求小明乘坐A路、E路车到学校的概率．

查看解析收藏纠错

+选题
16. 把长为2、宽为1的矩形如图依次摆放，恰使一个矩形的宽在另一个矩形的长的对称轴上，点A是格点（矩形的顶点为格点）．请在网格中完成下列画图（要求：①仅用无刻度的直尺：②保留必要的画图痕迹）．

（1）在图1中，画出 $\text{[math]}$ ，使 $\text{[math]}$ ，点B、C在格点上；

（2）在图2中，画出 $\text{[math]}$ 使 $\text{[math]}$ ，点B、C在格点上．

查看解析收藏纠错

+选题
17. 某超市以3元/本的价格购进某种笔记本若干，然后以5元/本的价格出售，每天售出20本．通过调查发现，这种笔记本的售价每降低0.1元，每天可多售出4本，为保证每天至少售出50本，该超市决定降价销售．

（1）若每本降价x元，则每天的销售量是本（用含x的代数式表示）．

（2）要想每天赢利60元，该超市需将每本的售价降低多少元？

查看解析收藏纠错

+选题
18. 随着互联网的高速发展，人们的支付方式发生了巨大改变，某学习小组抽样调查了春节期间某商场顾客的支付方式，主要有现金支付、银联卡支付和手机支付，调查得知使用这三种支付的人数比为 $\text{[math]}$ ，手机支付已成为市民购物便捷支付方式．手机支付主要有以下三种方式：A~支付宝，B~微信，C~其他．现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图．

（1）扇形统计图中， $\text{[math]}$ ；请补全条形统计图；

（2）若该商场春节期间共20000人购物，请估计用支付宝进行支付的人数．

（3）经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元，求这天顾客每笔交易的平均金额．

查看解析收藏纠错

+选题
19. 如图，在平面直角坐标系中，直线BC与y轴交于点A（0，4），与x轴交于点D ，点B ， C是反比例函数y＝ $\text{[math]}$ （x＞0）图象上的点，OB⊥BC于点B ， ∠BOD＝60°．

（1）求直线AB的解析式；

（2）求反比例函数的解析式；

（3）若△AOB的面积为S₁ ， △BOC的面积为S₂ ， △DOC的面积为S₃ ，直接写出S₁ ， S₂ ， S₃的一个数量关系式：

查看解析收藏纠错

+选题
20. 图1是某浴室花洒实景图，图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度，离地面CD的距离BC＝160cm.设花洒臂与墙面的夹角为α，可以扭动花洒臂调整角度，且花洒臂长AB＝30cm.假设水柱AE垂直AB直线喷射，小华在离墙面距离CD＝120cm处淋浴.

（1）当α＝30°时，水柱正好落在小华的头顶上，求小华的身高DE.

（2）如果小华要洗脚，需要调整水柱AE，使点E与点D重合，调整的方式有两种：
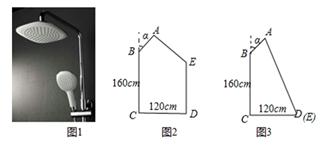
①其他条件不变，只要把活动调节点B向下移动即可，移动的距离BF与小华的身高DE有什么数量关系？直接写出你的结论；

②活动调节点B不动，只要调整α的大小，在图3中，试求α的度数.

（参考数据： $\text{[math]}$ ≈1.73，sin8.6°≈0.15，sin36.9°≈0.60，tan36.9°≈0.75）

查看解析收藏纠错

+选题
21. 如图，已知AB是⊙O的直径，BE是⊙O的弦，BC是∠ABE的平分线且交⊙O于点C ，连接AC ， CE ，过点C作CD⊥BE ，交BE的延长线于点D ．

（1） ∠DCE∠CBE；（填“＞”“＜”或“＝”）

（2）求证：DC是⊙O的切线；

（3）若⊙O的直径为10，sin∠BAC＝ $\text{[math]}$ ，求BE的长．

查看解析收藏纠错

+选题
22. 在下列正多边形中，O是中心，定义： $\text{[math]}$ 为相应正多边形的基本三角形．如图1， $\text{[math]}$ 是正三角形 $\text{[math]}$ 的基本三角形；如图2， $\text{[math]}$ 是正方形 $\text{[math]}$ 的基本三角形；如图3， $\text{[math]}$ 为正n边形 $\text{[math]}$ …的基本三角形．将基本 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ 角度得 $\text{[math]}$ ．

（1）若线段 $\text{[math]}$ 与线段 $\text{[math]}$ 相交点 $\text{[math]}$ ，则：
图1中 $\text{[math]}$ 的取值范围是；

图3中 $\text{[math]}$ 的取值范围是；

（2）在图1中，求证 $\text{[math]}$

（3）在图2中，正方形边长为4， $\text{[math]}$ ，边 $\text{[math]}$ 上的一点P旋转后的对应点为 $\text{[math]}$ ，若 $\text{[math]}$ 有最小值时，求出该最小值及此时 $\text{[math]}$ 的长度；

（4）如图3，当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
23. 抛物线C：y＝ $\text{[math]}$ x[a（x﹣1）+x+1]（a为任意实数）．

（1）无论a取何值，抛物线C恒过定点，．

（2）当a＝1时，设抛物线C在第一象限依次经过的整数点（横、纵坐标均为整数的点）为A₁ ， A₂ ， ……A_n ，将抛物线C沿着直线y＝x（x≥0）平移，将平移后的抛物线记为C_n ，抛物线C_n经过点A_n ， C_n的顶点坐标为M_n（n为正整数且n＝1，2，…，n ，例如n＝1时，抛物线C₁经过点A₁ ， C₁的顶点坐标为M₁）．
①抛物线C₂的解析式为　 ▲ 　，顶点坐标为　 ▲ 　．

②抛物线C₁上是否存在点P ，使得PM₁∥A₂M₂？若存在，求出点P的坐标，并判断四边形PM₁M₂A₂的形状；若不存在，请说明理由．

③直接写出M_n_﹣1 ， M_n两顶点间的距离：　 ▲ 　．

查看解析收藏纠错

+选题

江西省九江三中、东湖中学2020年中考数学3月模拟试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨