修改时间:2024-07-13 浏览次数:208 类型:期中考试
将这位战士看成一条线段,碉堡看成一点,示意图如下,你能根据示意图解释其中的道理吗?

下面是彤彤同学写出的不完整的已知和求证,请你补全已知和求证,并完成证明.
已知:如图, ,……….

求证:………..
证明:
数学活动课上,老师提出了如下问题:
如图1,已知 中,
是
边上的中线.

求证: .
智慧小组的证法如下:
证明:如图2,延长 至
,使
,
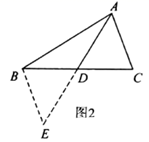
∵ 是
边上的中线∴
在 和
中
∴ (依据一)∴
在 中,
(依据二)
∴ .
依据1:;
依据2:.
任务二:如图3, ,
,则
的取值范围是;


试题篮