修改时间:2024-11-06 浏览次数:242 类型:中考模拟
a.甲、乙两校40名学生成绩的频数分布统计表如下:
|
成绩x 学校 |
| | | | |
| 甲 | 4 | 11 | 13 | 10 | 2 |
| 乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在 这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
| 学校 | 平均分 | 中位数 | 众数 |
| 甲 | 74.2 | n | 85 |
| 乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:

小石根据学习函数的经验,分别对函数 ,
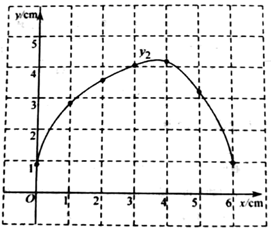
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
| x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| | 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| | 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
试题篮