修改时间:2024-07-31 浏览次数:319 类型:中考模拟
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
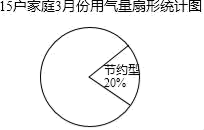
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
| 家庭人数 | 2 | 3 | 4 | 5 |
| 用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
| 用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
| 用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
例如:如图,当t=1时,原函数y=x,图象G所对应的函数关系式为y= .
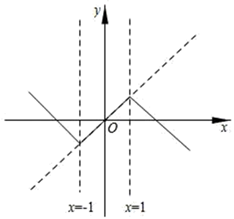
①图象G所对应的函数值y随x的增大而减小时,x的取值范围是.
②图象G所对应的函数是否有最大值,如果有,请求出最大值;如果没有,请说明理由.
①n=﹣1时,若图象G与直线y=2恰好有两个交点,求t的取值范围.
②当t=2时,若图象G在n2﹣2≤x≤n2﹣1上的函数值y随x的增大而减小,直接写出n的取值范围.
试题篮