2017年江苏省南京市玄武区中考数学二模试卷

修改时间：2024-07-12 浏览次数：386 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 2的相反数是（）

A . 2 B . $\text{[math]}$ C . ﹣2 D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 氢原子的半径大约是0.000 0077m，将数据0.000 0077用科学记数法表示为（）

A . 0.77×10^﹣⁵ B . 0.77×10^﹣⁶ C . 7.7×10^﹣⁵ D . 7.7×10^﹣⁶

查看解析收藏纠错

+选题
3. ﹣ $\text{[math]}$ 介于（）

A . ﹣4与﹣3之间 B . ﹣3与﹣2之间 C . ﹣2与﹣1之间 D . ﹣1与0之间

查看解析收藏纠错

+选题
4. 下列平面图形，既是中心对称图形，又是轴对称图形的是（）

A . 等腰三角形 B . 正五边形 C . 平行四边形 D . 矩形

查看解析收藏纠错

+选题
5. 如图是一个几何体的三视图，这个几何体是（）

A . 四棱柱 B . 三棱柱 C . 三棱锥 D . 圆锥

查看解析收藏纠错

+选题
6.
如图，正六边形ABCDEF的边长为6cm，P是对角线BE上一动点，过点P作直线l与BE垂直，动点P从B点出发且以1cm/s的速度匀速平移至E点．设直线l扫过正六边形ABCDEF区域的面积为S（cm²），点P的运动时间为t（s），下列能反映S与t之间函数关系的大致图象是（）

A . B . C . D .

查看解析收藏纠错

+选题

二、填空题

7. 8的算术平方根是；8的立方根是．

查看解析收藏纠错

+选题
8. 要使式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

查看解析收藏纠错

+选题
9. 计算 $\text{[math]}$ =．

查看解析收藏纠错

+选题
10. 已知反比例函数y= $\text{[math]}$ 的图象经过点A（﹣2，3），则当x=﹣1时，y=．

查看解析收藏纠错

+选题
11. 某班的中考英语口语考试成绩如表：
考试成绩/分
30
29
28
27
26
学生数/人
3
15
13
6
3
则该班中考英语口语考试成绩的众数比中位数多分．

查看解析收藏纠错

+选题
12. 若方程x²﹣12x+5=0的两根分别为a，b，则a²b+ab²的值为．

查看解析收藏纠错

+选题
13. 若圆锥的高是8cm，母线长是10cm，则这个圆锥的侧面积是cm²（结果保留π）．

查看解析收藏纠错

+选题
14. 若一个正多边形的每一个外角都是30°，则这个正多边形的边数为．

查看解析收藏纠错

+选题
15. 如图，在⊙O的内接六边形ABCDEF中，∠A+∠C=220°，则∠E=°．

查看解析收藏纠错

+选题
16. 如图，在△ABC中，∠A=45°，∠B=60°，AB=4，P是BC边上的动点（不与B，C重合），点P关于直线AB，AC的对称点分别为M，N，则线段MN长的取值范围是．

查看解析收藏纠错

+选题

三、解答题

17. 解答题

（1）解不等式组 $\text{[math]}$ 并把它的解集在数轴上表示出来．

（2）解方程 $\text{[math]}$ =1﹣ $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 先化简代数式1﹣ $\text{[math]}$ ÷ $\text{[math]}$ ，并从﹣1，0，1，3中选取一个合适的数代入求值．

查看解析收藏纠错

+选题
19. 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源，随机抽取部分学生了解情况，并将统计结果绘制成频数分布表及频数分布直方图．
上网查找学习资源方式频数分布表
查找方式
频数
频率
搜索引擎
16
32%
专题网站
15
a
在线网校
4
8%
试题题库
10
20%
其他
b
10%

（1）频数分布表中a，b的值：a=；b=；

（2）补全频数分布直方图；

（3）若全校有1000名学生，估计该校利用搜索引擎上网查找学习资源的学生有多少名？

查看解析收藏纠错

+选题
20. 从2名男生和3名女生中随机抽取运动会志愿者．求下列事件的概率：

（1）抽取1名，恰好是女生的概率为；

（2）抽取2名，恰好是1名男生和1名女生．

查看解析收藏纠错

+选题
21. 如图，在四边形ABCD中，BE⊥AC，DF⊥AC，垂足分别为E，F，BE=DF，AE=CF．

（1）求证：△AFD≌△CEB；

（2）若∠CBE=∠BAC，四边形ABCD是怎样的四边形？证明你的结论．

查看解析收藏纠错

+选题
22. 某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场采取了降价措施．假设在一定范围内，衬衫的单价每降1元，商场平均每天可多售出2件．如果降价后商场销售这批衬衫每天盈利1250元，那么衬衫的单价降了多少元？

查看解析收藏纠错

+选题
23. 如图，小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B，C两点的俯角分别为60°和35°，已知大桥BC的长度为100m，且与地面在同一水平面上．求热气球离地面的高度．
（结果保留整数，参考数据：sin35°≈ $\text{[math]}$ ，cos35°≈ $\text{[math]}$ ，tan35°≈ $\text{[math]}$ ， $\text{[math]}$ ≈1.7）

查看解析收藏纠错

+选题
24. 已知二次函数y=x²﹣（a﹣1）x+a﹣2，其中a是常数．

（1）求证：不论a为何值，该二次函数的图象与x轴一定有公共点；

（2）当a=4时，该二次函数的图象顶点为A，与x轴交于B，D两点，与y轴交于C点，求四边形ABCD的面积．

查看解析收藏纠错

+选题
25. 如图①，在一条笔直的公路上有M、P、N三个地点，M、P两地相距20km，甲开汽车，乙骑自行车分别从M、P两地同时出发，匀速前往N地，到达N地后停止运动．已知乙骑自行车的速度为20km/h，甲，乙两人之间的距离y（km）与乙行驶的时间t（h）之间的关系如图②所示．

（1） M、N两地之间的距离为km；

（2）求线段BC所表示的y与t之间的函数表达式；

（3）若乙到达N地后，甲，乙立即以各自原速度返回M地，请在图②所给的直角坐标系中补全函数图象．

查看解析收藏纠错

+选题
26. 如图，点A在⊙O上，点P是⊙O外一点，PA切⊙O于点A，连接OP交⊙O于点D，作AB⊥OP于点C，交⊙O于点B，连接PB．

（1）求证：PB是⊙O的切线；

（2）若PC=9，AB=6 $\text{[math]}$ ，
①求图中阴影部分的面积；

查看解析收藏纠错

+选题
27. 解答题

（1）
问题背景
如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重合），求证： $\text{[math]}$ PA=PB+PC．
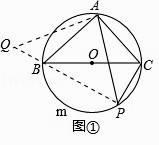
小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：
第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；
第二步：证明Q，B，P三点共线，进而原题得证．
请你根据小明同学的思考过程完成证明过程．

（2）
类比迁移

如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．

（3）
拓展延伸
如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB= $\text{[math]}$ AC，AB⊥AC，垂足为A，则OC的最小值为．

查看解析收藏纠错

+选题

查找方式	频数	频率
搜索引擎	16	32%
专题网站	15	a
在线网校	4	8%
试题题库	10	20%
其他	b	10%

考试成绩/分	30	29	28	27	26
学生数/人	3	15	13	6	3

2017年江苏省南京市玄武区中考数学二模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨