修改时间:2024-07-12 浏览次数:1100 类型:期中考试
如图,有足够多的边长为a的小正方形(A类)、宽为a长为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料若干可以拼出一些长方形来解释某些等式.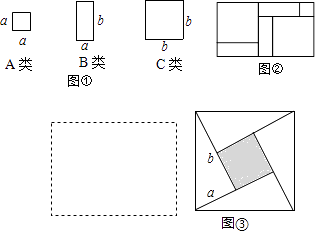
尝试解决:
拓展研究:如图③,大正方形的边长为m,小正方形的边长为n,若用m、n表示四个直角三角形的两直角边边长(b>a),观察图案,以下关系式中正确的有.(填写正确选项的序号)
(1)ab=
(2)a+b=m
(3)a2+b2=
(4)a2+b2=m2
试题篮