修改时间:2024-07-13 浏览次数:516 类型:中考模拟
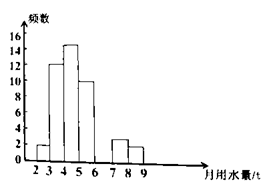
|
月均用水量(单位:t) |
频数 |
百分比 |
|
2≤x<3 |
2 |
4% |
|
3≤x<4 |
12 |
24% |
|
4≤x<5 |
||
|
5≤x<6 |
10 |
20% |
|
6≤x<7 |
12% |
|
|
7≤x<8 |
3 |
6% |
|
8≤x<9 |
2 |
4% |

当0≤t≤20,y=;当20<t≤40时,y=;


试题篮