2016-2017学年江西省景德镇市昌江区八年级下学期期中数学试卷

修改时间：2024-07-12 浏览次数：1112 类型：期中考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（）

A . 50° B . 100° C . 120° D . 130°

查看解析收藏纠错

+选题
2. 若不等式组 $\text{[math]}$ 恰有两个整数解，则m的取值范围是（）

A . ﹣1≤m＜0 B . ﹣1＜m≤0 C . ﹣1≤m≤0 D . ﹣1＜m＜0

查看解析收藏纠错

+选题
3. 如图，用一个半径为5cm的定滑轮带动重物上升，滑轮上一点A旋转了108°，假设绳索（粗细不计）与滑轮之间没有滑动，则重物上升了（）

A . πcm B . 2πcm C . 3πcm D . 5πcm

查看解析收藏纠错

+选题
4. 如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（）

A . 15° B . 17.5° C . 20° D . 22.5°

查看解析收藏纠错

+选题
5. 如图，一次函数y₁=x+b与y₂=kx﹣2的图象相交于点P（1，3），则关于x的不等式x+b＞kx+4的解集是（）

A . x＞﹣2 B . x＞0 C . x＞1 D . x＜1

查看解析收藏纠错

+选题
6. 如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A₁B₁C，当A₁落在AB边上时，连接B₁B，取BB₁的中点D，连接A₁D，则A₁D的长度是（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . 3 D . 2 $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

7. 若点P（a，4﹣a）是第一象限的点，则a的取值范围是．

查看解析收藏纠错

+选题
8. 如图，在Rt△ABC中，E是斜边AB的中点，若AB=10，则CE=．

查看解析收藏纠错

+选题
9. 点P（2，﹣3）先向左平移4个单位长度，再向上平移1个单位长度，得到点P′的坐标是．

查看解析收藏纠错

+选题
10. 对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到“结果是否大于88？”为一次操作．如果操作只进行一次就停止，则x的取值范围是．

查看解析收藏纠错

+选题
11. 如图，正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG，EF与AD相交于点H，延长DA交GF于点K．若正方形ABCD边长为 $\text{[math]}$ ，则AK=．

查看解析收藏纠错

+选题
12. 等腰三角形一腰上的高与另一腰的夹角为48°，则该等腰三角形的底角的度数为．

查看解析收藏纠错

+选题

三、解答题

13. 解答题

（1）求不等式组 $\text{[math]}$ 的解集；

（2）如图，在△ABC中，已知∠ABC=30°，将△ABC绕点B逆时针旋转50°后得到△A′BC′，已知A′C′∥BC，求∠A的度数．

查看解析收藏纠错

+选题
14. x取哪些整数值时，不等式5x+2＞3（x﹣1）与 $\text{[math]}$ x≤2﹣ $\text{[math]}$ 都成立？

查看解析收藏纠错

+选题
15. 如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．

查看解析收藏纠错

+选题
16. 如图，△ABC中，∠C=90°，点D在AC上，已知∠BDC=45°，BD=10 $\text{[math]}$ ，AB=20．求∠A的度数．

查看解析收藏纠错

+选题
17. 如图，在6×6的方格中，点A，O，B都在小方格的顶点上，请在方格中取点C和D，画△AOC和△BOD，使这两个三角形全等．

（1）在图1中画出的两个三角形，可以使其中一个三角形通过轴对称得到另一个三角形．

（2）在图2中画出的两个三角形，可以使其中一个三角形通过旋转得到另一个三角形．

查看解析收藏纠错

+选题
18. 如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O

（1）求证：OB=OC；

（2）若∠ABC=50°，求∠BOC的度数．

查看解析收藏纠错

+选题
19. 按要求作图

（1）
已知△ABC中，∠A=90°，∠B=67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，把所有不同的分割方法都画出来．只需画图，不必说明理由，但要在图中标出相等两角的度数）

（2）已知△ABC中，∠C是其最小的内角，过顶点B的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC与∠C之间的关系．

查看解析收藏纠错

+选题
20. 某职业高中机电班共有学生42人，其中男生人数比女生人数的2倍少3人．

（1）该班男生和女生各有多少人？

（2）某工厂决定到该班招录30名学生，经测试，该班男、女生每天能加工的零件数分别为50个和45个，为保证他们每天加工的零件总数不少于1460个，那么至少要招录多少名男学生？

查看解析收藏纠错

+选题
21. 如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．

（1）求证：EF= $\text{[math]}$ AC．

（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．

查看解析收藏纠错

+选题
22. 如图，已知，在△ABC中，CA=CB，∠ACB=90°，E，F分别是CA，CB边的三等分点，将△ECF绕点C逆时针旋转α角（0°＜α＜90°），得到△MCN，连接AM，BN．

（1）求证：AM=BN；

（2）当MA∥CN时，试求旋转角α的余弦值．

查看解析收藏纠错

+选题
23. 如图1，已知△ABC中，AB=BC=1，∠ABC=90°，把一块含30°角的三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．

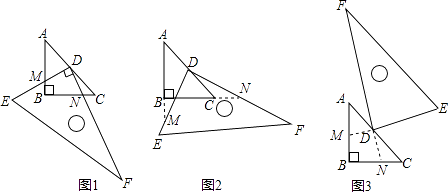
（1）在图1中，DE交AB于M，DF交BC于N．①证明DM=DN；②在这一过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的；若不发生变化，求出其面积；

（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM=DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM=DN是否仍然成立？若成立，请给出写出结论，不用证明．

查看解析收藏纠错

+选题

2016-2017学年江西省景德镇市昌江区八年级下学期期中数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨