浙江绍兴2017年初三中考模拟数学试卷

1. 在：0，﹣2，1， $\text{[math]}$ 这四个数中，最小的数是（）

A . $\text{[math]}$ B . 1 C . ﹣2 D . 0

查看解析收藏纠错

+选题
2. 如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算结果正确的是（）

A . a²•a³=a⁶ B . （a²）³=a⁵ C . a²+3a²=4a⁴ D . a⁴÷a²=a²

查看解析收藏纠错

+选题
4. 化简： $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6.
如图，已知⊙O与直线 $\text{[math]}$ 相切于点A 点，点P，Q同时从A出发，P沿着直线 $\text{[math]}$ 向右，Q沿着圆周按逆时针以相同的速度运动，当Q运动到点A时，点P也停止运动．连接OQ、OP（如图），则阴影部分面积S₁、S₂的大小关系是（）

A . S₁=S₂ B . S₁≤S₂ C . S₁≥S₂ D . 先S₁<S₂ ，再S₁=S₂ ，最后S₁>S₂

查看解析收藏纠错

+选题
7.
如图，四边形EFGH是矩形ABCD的内接矩形，且EF：FG=3：1，AB：BC=2：1，则tan∠AHE的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8.
如图，反比例函数y= $\text{[math]}$ 的图象经过二次函数y=ax²+bx图象的顶点（ $\text{[math]}$ ，m）（m＞0），则有（）

A . a=b+2k B . a=b﹣2k C . k＜b＜0 D . a＜k＜0

查看解析收藏纠错

+选题
9.
我们把钟表的时针、分针及两针尖所连线段所围成的图形面积叫做这个钟表的该时刻面积．如图，△AOB的面积即为该钟表8点30分的时刻面积，那么从9时到10时，钟表的时刻面积等于该钟表8点30分的时刻面积的时刻数有（）

A . 4个 B . 3个 C . 2个 D . 1个

查看解析收藏纠错

+选题

10. 因式分解： $\text{[math]}$ ．

查看解析收藏纠错

+选题
11. 不等式组 $\text{[math]}$ 的解是．

查看解析收藏纠错

+选题
12.
如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC
互补，则弦BC的长为．

查看解析收藏纠错

+选题
13.
如图，点A、B为直线 $\text{[math]}$ 上的两点，过A、B两点分别作 $\text{[math]}$ 轴平行线交反比例函数 $\text{[math]}$ 的图象于点C、D两点，若BD=3AC，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
14.
如图，将一条长为60cm的卷尺铺平后折叠，使得卷尺自身的一部分重合，然后在重合部分（阴影处）沿与卷尺边垂直的方向剪一刀，此时卷尺分为了三段，若这三段长度由短到长的比为1：2：3，则折痕对应的刻度为．

查看解析收藏纠错

+选题
15. 一个大的等腰三角形能被分割为两个小等腰三角形，则该大等腰三角形顶角的度数是．

查看解析收藏纠错

+选题

16. 计算.

（1）计算： $\text{[math]}$ + $\text{[math]}$ － $\text{[math]}$ － $\text{[math]}$ ．

（2）先化简，再求值：a（a﹣2b）+（a+b）² ，其中a=﹣1，b= $\text{[math]}$ ．

查看解析收藏纠错

+选题
17.
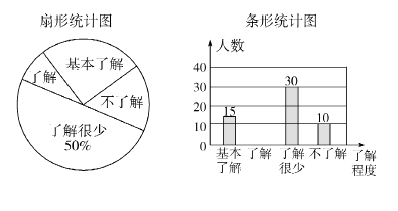
“校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

（1）接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为；并)请补全条形统计图；

（2）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为；

（3）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

查看解析收藏纠错

+选题
18.
某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如折线图所示：根据图象解答下列问题：

（1）洗衣机的进水时间是分钟；清洗时洗衣机中的水量是升；

（2）已知洗衣机的排水速度为每分钟19升，
①求排水时y与x之间的关系式．
②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量．

查看解析收藏纠错

+选题
19.
“低碳环保，你我同行”．两年来，绍兴市区的公共自行车给市民出行带来切实方便．如图1所示是一辆自行车的实物图．车架档AC与CD的长分别为45cm，60cm，且它们互相垂直，座杆CE的长为20cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2，图3是公共自行车车桩的截面示意图，PQ⊥PM，PM⊥MN，点Q，N在GO上，GO∥HF，PQ=80cm，PM=24cm，QN=25cm，GH=4cm.

（1）求车架档AD的长；

（2）求车座点E到车架档AB的距离及车桩的截面示意图中的点P到地面的距离．
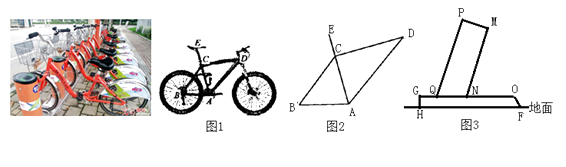
（结果精确到1cm．参考数据：sin75°≈0.97，cos75°≈0.26，tan75≈3.73）

查看解析收藏纠错

+选题
20.
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，交OA于点F，连接EF并延长EF交AB于G，且EG⊥AB．

（1）求证：直线AB是⊙O的切线；

（2）若EF=2FG，AB= $\text{[math]}$ ，求图中阴影部分的面积；

（3）若EG=9，BG=12，求BD的长．

查看解析收藏纠错

+选题
21.
我们给出如下定义：在平面直角坐标系xOy中，如果一条抛物线平移后得到的抛物线经过原抛物线的顶点，那么这条抛物线叫做原抛物线的过顶抛物线．如下图，抛物线F₂都是抛物线F₁的过顶抛物线，设F₁的顶点为A，F₂的对称轴分别交F₁、F₂于点D、B，点C是点A关于直线BD的对称点．

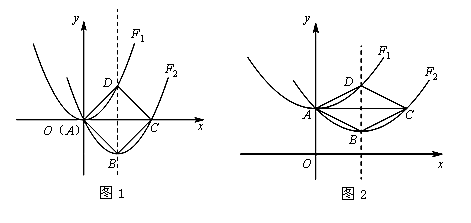
（1）如图1，如果抛物线y=x²的过顶抛物线为y=ax²+bx，C（2，0），那么①a=，b=．
②如果顺次连接A、B、C、D四点，那么四边形ABCD为
A．平行四边形 B．矩形 C．菱形 D．正方形

（2）如图2，抛物线y=ax²+c的过顶抛物线为F₂ ， B（2，c-1）．求四边形ABCD的面积．

（3）如果抛物线 $\text{[math]}$ 的过顶抛物线是F₂ ，四边形ABCD的面积为 $\text{[math]}$ ，请直接写出点B的坐标．答：．

查看解析收藏纠错

+选题
22.
在矩形ABCD中，AB=4，AD=6，P是AD边的中点，点E在AB边上，EP的延
长线交射线CD于F点，过点P作PQ⊥EF与射线BC相交于点Q．

（1）如图1，当点Q在点C时，试求AE的长．

（2）如图2，点G为FQ的中点，连结PG．
当AE=1时，求PG的长．

（3）当点E从点A运动到点B时，试直接写出线段PG扫过的面积．

查看解析收藏纠错

+选题
23.
如图，在矩形ABCO中，点O为坐标原点，点A、C在坐标轴上，点B的坐标为（7，3），点D在y轴上，且D与A关于原点对称，直线与x轴交于点E，点F（m，-4）在直线上，连结DE、DF.

（1）请直接写出F的坐标和△DEF的形状；答：、．

（2）若点P在矩形ABCO的边BC上，过F作FG⊥x轴于G.
若线段EF上有一点M，使∠MDF=∠GFE，请求出M的坐标；

（3）若直线EF上有一点Q，使△APQ是等腰直角三角形，请直接写出满足条件的Q的坐标.
答：．

查看解析收藏纠错

+选题

浙江绍兴2017年初三中考模拟数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

浙江绍兴2017年初三中考模拟数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨