广东省深圳市2018-2019学年八年级下学期数学第一次月考模拟卷

修改时间：2019-03-27 浏览次数：430 类型：月考试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 如图，在△ABC中，AB=AC，过A点作AD∥BC，若∠BAD=110°，则∠BAC的大小为（）

A . 30° B . 40° C . 50° D . 70°

查看解析收藏纠错

+选题
2. 已知等腰三角形的一边等于3，一边等于6，那么它的周长等于（）

A . 12 B . 12或15 C . 15 D . 15或18

查看解析收藏纠错

+选题
3. 三角形内，到三角形三边距离相等的点是（）

A . 三角形三条角平分线的交点 B . 三角形三条中线的交点 C . 三角形三条高（或高所在直线）的交点 D . 三角形三边中垂线的交点

查看解析收藏纠错

+选题
4. 等腰三角形的两条边长分别为3cm，7cm，则等腰三角形的周长为（）cm

A . 13或17 B . 17 C . 13 D . 10

查看解析收藏纠错

+选题
5. 若a－b＜0，则下列各式中一定正确的是（）

A . a＞b B . ab＞0 C . $\text{[math]}$ D . －a＞－b

查看解析收藏纠错

+选题
6. 在四川抗震救灾中，某抢险地段需实行爆破.操作人员点燃导火线后，要在炸药爆炸前跑到400 m以外的安全区域.已知导火线的燃烧速度是1.2 cm/s，操作人员跑步的速度是5 m/s.为了保证操作人员的安全，导火线的长度要超过（）

A . 66 cm B . 76 cm C . 86 cm D . 96 cm

查看解析收藏纠错

+选题
7. 不等式（1﹣a） x＞2变形后得到 $\text{[math]}$ 成立，则a的取值（）

A . a＞0 B . a＜0 C . a＞1 D . a＜1

查看解析收藏纠错

+选题
8.
如图，在△ACB中AB=AC=6，BC=4.5，分别以点A、B为圆心，4为半径画圆弧，交于两点，过这两点的直线交AC于点D，连接BD，则△BCD的周长为（　　）

A . 10 B . 6 C . 10.5 D . 8

查看解析收藏纠错

+选题
9.
如图，对正方形纸片ABCD进行如下操作：
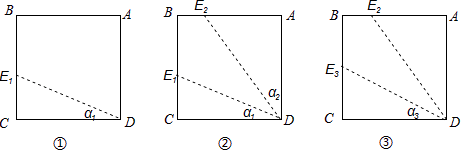
（I）过点D任作一条直线与BC边相交于点E₁（如图①），记∠CDE₁=a₁；
（II）作∠ADE₁的平分线交AB边于点E₂（如图②），记∠ADE₂=a₂；
（III）作∠CDE₂的平分线交BC边于点E₃（如图③），记∠CDE₃=a₃；
按此作法从操作（2）起重复以上步骤，得到a₁ ， a₂ ， …，a_n ， …，现有如下结论：
①当a₁=10°时，a₂=40°；
②2a₄+a₃=90°；
③当a₅=30°时，△CDE₉≌△ADE₁₀；
④当a₁=45°时，BE₂= $\text{[math]}$ AE₂ ．
其中正确的个数为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
10.
如图，在△ABC中，AB＞AC ，分别以点B和点C为圆心，大于BC一半的长为半径作圆弧，两弧相交于点M和点N ，作直线MN交AB于点D；连结CD.若AB＝7，AC＝5，则△ACD的周长为（）

A . 2 $\text{[math]}$ B . 12 C . 17 D . 19

查看解析收藏纠错

+选题
11. 一次函数y = kx + 4的图象与坐标轴围成的三角形的面积为4，则k的值为（）．

A . 2 B . −2 C . ±2 D . 不存在

查看解析收藏纠错

+选题
12. 不等式组 $\text{[math]}$ 的最小整数解为（）

A . ﹣1 B . 0 C . 1 D . 2

查看解析收藏纠错

+选题

二、填空题

13. 如图，一次函数y=ax+b的图象经过A（2，0）、B（0，﹣1）两点，则关于x的不等式ax+b＜0的解集是．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于M，N两点；
②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为．

查看解析收藏纠错

+选题
15.
如图，∠AOB=45°，过OA上到点O的距离分别为1，3，5，7，9，11，13……的点OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为S₁ ， S₂ ， S₃ ， S₄……．则第一个黑色梯形的面积S₁=；观察图中的规律，第n(n为正整数)个黑色梯形的面积S_n=．

查看解析收藏纠错

+选题
16.
如图，已知函数y=﹣2x+4，观察图象回答下列问题
（1）x 时，y＞0；（2）x 时，y＜0；
（3）x 时，y=0；（4）x 时，y＞4．

查看解析收藏纠错

+选题

三、解答题

17. 问题情境：如图1，点D是△ABC外的一点，点E在BC边的延长线上，BD平分∠ABC，CD平分∠ACE．试探究∠D与∠A的数量关系．

（1）特例探究：
如图2，若△ABC是等边三角形，其余条件不变，则∠D＝；

如图3，若△ABC是等腰三角形，顶角∠A＝100°，其余条件不变，则∠D＝；这两个图中，∠D与∠A度数的比是；

（2）猜想证明：
如图1，△ABC为一般三角形，在（1）中获得的∠D与∠A的关系是否还成立？若成立，利用图1证明你的结论；若不成立，说明理由．

查看解析收藏纠错

+选题
18. 如图，已知B，C，E三点在同一条直线上，△ABC与△DCE都是等边三角形，其中线段BD交AC于点G，线段AE交CD于点F.

求证：

（1） △ACE≌△BCD；

（2） $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 直线y=2x﹣1与直线y=x+4的交点是，故当x时，直线y=2x﹣l上的点在直线y=x+4上相应点的上方；当x时，直线y=2x﹣1上的点在直线y=x+4上相应点的下方．

查看解析收藏纠错

+选题
20. 解不等式组 $\text{[math]}$ ，并写出不等式组的整数解．

查看解析收藏纠错

+选题
21. 某文具商店销售功能相同的两种品牌的计算器，购买2个A品牌和1个B品牌的计算器共需122元；购买1个A品牌和2个B品牌的计算器共需124元．

（1）求这两种品牌计算器的单价；

（2）学校开学前夕，该商店举行促销活动，具体办法如下：购买A品牌计算器按原价的九折销售，购买B品牌计算器超出10个以上超出的部分按原价的八折销售，①设购买x个A品牌的计算器需要y₁元，购买x个B品牌的计算器需要y₂元，分别求出y₁、y₂关于x的函数关系式；
②小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过10个，问购买哪种品牌的计算器更合算？请说明理由．

查看解析收藏纠错

+选题
22. △ABC在平面直角坐标系xOy中的位置如图所示．

（1） ①作△ABC关于点C成中心对称的△A₁B₁C₁；②将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂ ．

（2）在x轴上求作一点P，使 $\text{[math]}$ 的值最小，并写出点P的坐标（不写解答过程，直接写出结果）

查看解析收藏纠错

+选题
23. 如图在四边形ABCD中AB=BC= $\text{[math]}$ ，CD= $\text{[math]}$ ，AD=1且AB $\text{[math]}$ CB试求四边形ABCD的面积（提示：连接AC）。

查看解析收藏纠错

+选题
24. 把文字翻译成数学符号，构建方程组模型是解此类题的关键；方案型问题就是要构建双边不等式，有几个整数解就有几种方案.某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．

（1）求每辆A型车和B型车的售价各为多少元．

（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？

查看解析收藏纠错

+选题

广东省深圳市2018-2019学年八年级下学期数学第一次月考模拟卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨