2016-2017学年浙江省杭州市萧山区党湾中学八年级下学期开学数学试卷

1. 已知三角形的两边长分别为8和4，则第三边长可能是（）

A . 3 B . 4 C . 8 D . 12

查看解析收藏纠错

+选题
2. 平面直角坐标系内有一点A（a，﹣a），若a＞0，则点A位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

查看解析收藏纠错

+选题
3. 若m＞n，则下列不等式成立的是（）

A . ﹣3m＞﹣2n B . am＞an C . a²m＞a²n D . m﹣3＞n﹣3

查看解析收藏纠错

+选题
4. 在圆周长计算公式C=2πr中，对半径不同的圆，变量有（　　）

A . C，r B . C，π，r C . C，πr D . C，2π，r

查看解析收藏纠错

+选题
5. 如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（）

A . AB=CD B . EC=BF C . ∠A=∠D D . AB=BC

查看解析收藏纠错

+选题
6. 在△ABC中，AB=AC=5，BC=6，AD平分∠BAC交BC于点D，则BC边上的高线长是（　　）

A . 3 B . 3.6 C . 4 D . 4.8

查看解析收藏纠错

+选题
7. 等腰三角形的一个内角为70°，它的一腰上的高与底边所夹的角的度数是（　　）

A . 35° B . 20° C . 35°或20° D . 无法确定

查看解析收藏纠错

+选题
8. 在下列四组点中，可以在同一个正比例函数图象上的一组点是（）

A . （2，﹣3），（﹣4，6） B . （﹣2，3），（4，6） C . （﹣2，﹣3），（4，﹣6） D . （2，3），（﹣4，6）

查看解析收藏纠错

+选题
9. 如图，Rt△ABC中，AC=BC=4，点D，E分别是AB，AC的中点，在CD上找一点P，使PA+PE最小，则这个最小值是（）

A . 2 B . $\text{[math]}$ C . 2 $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
10. 如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：
①△AED≌△AEF
②△AED为等腰三角形
③BE+DC＞DE
④BE²+DC²=DE² ，
其中正确的有（）个．

A . 4 B . 3 C . 2 D . 1

查看解析收藏纠错

+选题

11. 化简 $\text{[math]}$ =．

查看解析收藏纠错

+选题
12. 在平面直角坐标系中，点（﹣1，2）关于y轴对称的点的坐标是．

查看解析收藏纠错

+选题
13. 已知A（1，1）是平面直角坐标系内一点，若以y轴的正方向为正北方向，以x轴的正方向为正东方向，则点A位于坐标原点O的度方向，与点O的距离为．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，D是BC上一点，AC=CD，∠DAB=10°，则∠CAB﹣∠B=．

查看解析收藏纠错

+选题
15. 不等式组 $\text{[math]}$ 的解集是x＞2，则m的取值范围是．

查看解析收藏纠错

+选题
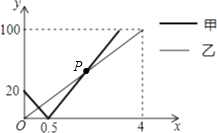
16. 沿河岸有A，B，C三个港口，甲、乙两船同时分别从A，B港口出发，匀速驶向C港，最终到达C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y₁、y₂（km），y₁、y₂与x的函数关系如图所示．考察下列结论：
①甲船的速度是25km/h；
②从A港到C港全程为120km；
③甲船比乙船早1.5小时到达终点；
④图中P点为两者相遇的交点，P点的坐标为（ $\text{[math]}$ ）；
⑤如果两船相距小于10km能够相互望见，那么，甲、乙两船可以相互望见时，x的取值范围是 $\text{[math]}$ ＜x＜2．
其中正确的结论有．

查看解析收藏纠错

+选题

17. 解不等式 $\text{[math]}$ ＜1﹣ $\text{[math]}$ ，并求出它的非负整数解．

查看解析收藏纠错

+选题
18. 如图，点C是∠ABC一边上一点

（1）按下列要求进行尺规作图：
①作线段BC的中垂线DE，E为垂足．
②作∠ABC的平分线BD．
③连结CD，并延长交BA于F．

（2）若∠ABC=62°，求∠BFC的度数．

查看解析收藏纠错

+选题
19.
如图，在平面直角坐标系xOy中，已知A（﹣1，2），B（﹣3，1）C（0，﹣1）

（1）在图中作出△ABC关于y轴的对称图形△A₁B₁C₁

（2）若将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是．

（3） AC的长等于，△ABC的面积是．

查看解析收藏纠错

+选题
20. 某校为开展好大课间活动，欲购买单价为20元的排球和单价为80元的篮球共100个．

（1）设购买排球数为x（个），购买两种球的总费用为y（元），请你写出y与x的函数关系式（不要求写出自变量的取值范围）；

（2）如果购买两种球的总费用不超过6620元，并且篮球数不少于排球数的3倍，那么有哪几种购买方案？

（3）从节约开支的角度来看，你认为采用哪种方案更合算？

查看解析收藏纠错

+选题
21. 如图，一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A（m，2），与y轴的交点为C，与x轴的交点为D．

（1） m=；

（2）若一次函数图象经过点B（﹣2，﹣1），求一次函数的解析式；

（3）在（2）的条件下，求△AOD的面积．

查看解析收藏纠错

+选题
22. 在直线上顺次取A，B，C三点，分别以AB，BC为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为D，E．

（1）如图①，连结CD，AE，求证：CD=AE；

（2）如图②，若AB=1，BC=2，求DE的长；

（3）如图③，将图②中的正三角形BEC绕B点作适当的旋转，连结AE，若有DE²+BE²=AE² ，试求∠DEB的度数．

查看解析收藏纠错

+选题
23.
A（0，4）是直角坐标系y轴上一点，P是x轴上一动点，从原点O出发，沿正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．

（1）若AB∥x轴，求t的值；

（2）设点B的坐标为（x，y），试求y关于x的函数表达式；

（3）当t=3时，平面直角坐标系内有一点M（3，a），请直接写出使△APM为等腰三角形的点M的坐标．

查看解析收藏纠错

+选题

2016-2017学年浙江省杭州市萧山区党湾中学八年级下学期开学数学试卷

一、仔细选一选

二、认真填一填

三、全面答一答

相关试卷收起∨

2016-2017学年浙江省杭州市萧山区党湾中学八年级下学期开学数学试卷

一、仔细选一选

二、认真填一填

三、全面答一答

相关试卷 收起∨

相关试卷收起∨