2015年浙江省衢州市中考数学试卷

1. ﹣3的相反数是（）

A . 3 B . ﹣3 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 一个几何体零件如图所示，则它的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算正确的是（　　）

A . a³+a³=2a⁶ B . （x²）³=x⁵ C . 2a⁶÷a³=2a² D . x³•x²=x⁵

查看解析收藏纠错

+选题
4. 如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（）

A . 8cm B . 6cm C . 4cm D . 2cm

查看解析收藏纠错

+选题
5. 某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，则这组数据的中位数是（　　）

A . 7 B . 6 C . 5 D . 4

查看解析收藏纠错

+选题
6. 下列四个函数图象中，当x＞0时，y随x的增大而减小的是（）

A . B . C . D .

查看解析收藏纠错

+选题
7.
数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（　　）

A . 勾股定理 B . 直径所对的圆周角是直角 C . 勾股定理的逆定理 D . 90°的圆周角所对的弦是直径

查看解析收藏纠错

+选题
8. 如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（）

A . 6 $\text{[math]}$ 米 B . 6米 C . 3 $\text{[math]}$ 米 D . 3米

查看解析收藏纠错

+选题
9. 如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tanα= $\text{[math]}$ ，则“人字梯”的顶端离地面的高度AD是（）

A . 144cm B . 180cm C . 240cm D . 360cm

查看解析收藏纠错

+选题
10. 如图，已知△ABC，AB=BC，以AB为直径的圆交AC于点D，过点D的⊙O的切线交BC于点E．若CD=5，CE=4，则⊙O的半径是（）

A . 3 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 从小明、小聪、小惠和小颖四人中随机选取1人参加学校组织的敬老活动，则小明被选中的概率是．

查看解析收藏纠错

+选题
12. 如图，小聪与小慧玩跷跷板，跷跷板支架高EF为0.6米，E是AB的中点，那么小聪能将小慧翘起的最大高度BC等于米．

查看解析收藏纠错

+选题
13. 一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽CD等于 m．

查看解析收藏纠错

+选题
14.
已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是．

查看解析收藏纠错

+选题
15.
如图，已知直线y=﹣ $\text{[math]}$ x+3分别交x轴、y轴于点A、B，P是抛物线y=﹣ $\text{[math]}$ x²+2x+5的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=﹣ $\text{[math]}$ x+3于点Q，则当PQ=BQ时，a的值是．

查看解析收藏纠错

+选题

16. 计算： $\text{[math]}$ ﹣|﹣2|+ $\text{[math]}$ ﹣4sin60°．

查看解析收藏纠错

+选题
17. 先化简，再求值：（x²﹣9）÷ $\text{[math]}$ ，其中x=﹣1．

查看解析收藏纠错

+选题
18. 如图，已知点A（a，3）是一次函数y₁=x+b图象与反比例函数y₂= $\text{[math]}$ 图象的一个交点．

（1）求一次函数的解析式；

（2）在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围．

查看解析收藏纠错

+选题
19. 某校在开展读书交流活动中全体师生积极捐书．为了解所捐书籍的种类，对部分书籍进行了抽样调查，李老师根据调查数据绘制了如图所示不完整统计图．请根据统计图回答下面问题：

（1）本次抽样调查的书籍有多少本？请补全条形统计图；

（2）求出图1中表示文学类书籍的扇形圆心角度数；

（3）本次活动师生共捐书1200本，请估计有多少本科普类书籍？

查看解析收藏纠错

+选题
20. 如图1，将矩形ABCD沿DE折叠，使顶点A落在DC上的点A′处，然后将矩形展平，沿EF折叠，使顶点A落在折痕DE上的点G处．再将矩形ABCD沿CE折叠，此时顶点B恰好落在DE上的点H处．如图2．

（1）求证：EG=CH；

（2）已知AF= $\text{[math]}$ ，求AD和AB的长．

查看解析收藏纠错

+选题
21. 小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a₁x²+b₁x+c₁（a₁≠0，a₁ ， b₁ ， c₁是常数）与y=a₂x²+b₂x+c₂（a₂≠0，a₂ ， b₂ ， c₂是常数）满足a₁+a₂=0，b₁=b₂ ， c₁+c₂=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x²+3x﹣2的“旋转函数”．
小明是这样思考的：由函数y=﹣x²+3x﹣2可知，a₁=﹣1，b₁=3，c₁=﹣2，根据a₁+a₂=0，b₁=b₂ ， c₁+c₂=0，求出a₂ ， b₂ ， c₂ ，就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：

（1）写出函数y=﹣x²+3x﹣2的“旋转函数”；

（2）若函数y=﹣x²+ $\text{[math]}$ mx﹣2与y=x²﹣2nx+n互为“旋转函数”，求（m+n）²⁰¹⁵的值；

（3）已知函数y=﹣ $\text{[math]}$ （x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A₁ ， B₁ ， C₁ ，试证明经过点A₁ ， B₁ ， C₁的二次函数与函数y=﹣ $\text{[math]}$ （x+1）（x﹣4）互为“旋转函数．”

查看解析收藏纠错

+选题
22. 高铁的开通，给衢州市民出行带来了极大的方便，“五一”期间，乐乐和颖颖相约到杭州市的某游乐园游玩，乐乐乘私家车从衢州出发1小时后，颖颖乘坐高铁从衢州出发，先到杭州火车站，然后再转车出租车去游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开衢州的距离y（千米）与乘车时间t（小时）的关系如图所示．
请结合图象解决下面问题：

（1）高铁的平均速度是每小时多少千米？

（2）当颖颖达到杭州火车东站时，乐乐距离游乐园还有多少千米？

（3）若乐乐要提前18分钟到达游乐园，问私家车的速度必须达到多少千米/小时？

查看解析收藏纠错

+选题
23.
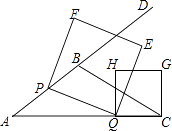
如图，在△ABC中，AB=5，AC=9，S_△_ABC= $\text{[math]}$ ，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．

（1）求tanA的值；

（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；

（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．

查看解析收藏纠错

+选题

2015年浙江省衢州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

2015年浙江省衢州市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨