修改时间:2021-05-20 浏览次数:985 类型:中考真卷


请解答下列问题:
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||

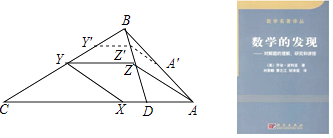
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ .
同理可得 .∴
.
∵Z'A'=Y'Z',∴ZA=YZ.
任务:
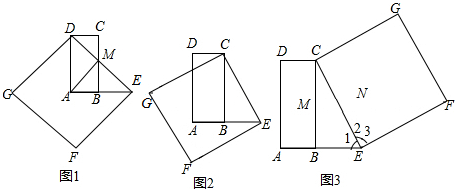
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴ .(依据1)
∵BE=AB,∴ .∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
探索发现:
试题篮