江苏省镇江市2018年中考数学试卷

修改时间：2024-07-13 浏览次数：937 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、填空题

1. ﹣8的绝对值是．

查看解析收藏纠错

+选题
2. 一组数据2，3，3，1，5的众数是．

查看解析收藏纠错

+选题
3. 计算：（a²）³=．

查看解析收藏纠错

+选题
4. 分解因式：x²﹣1=．

查看解析收藏纠错

+选题
5. 若分式 $\text{[math]}$ 有意义，则x的取值范围是．

查看解析收藏纠错

+选题
6. 计算： $\text{[math]}$ =．

查看解析收藏纠错

+选题
7. 圆锥底面圆的半径为1，侧面积等于3π，则它的母线长为．

查看解析收藏纠错

+选题
8. 反比例函数y= $\text{[math]}$ （k≠0）的图象经过点A（﹣2，4），则在每一个象限内，y随x的增大而．（填“增大”或“减小”）

查看解析收藏纠错

+选题
9. 如图，AB为△ADC的外接圆⊙O的直径，若∠BAD=50°，则∠ACD=°．

查看解析收藏纠错

+选题
10. 已知二次函数y=x²﹣4x+k的图象的顶点在x轴下方，则实数k的取值范围是．

查看解析收藏纠错

+选题
11. 如图，△ABC中，∠BAC＞90°，BC=5，将△ABC绕点C按顺时针方向旋转90°，点B对应点B′落在BA的延长线上．若sin∠B′AC= $\text{[math]}$ ，则AC=．

查看解析收藏纠错

+选题
12. 如图，点E、F、G分别在菱形ABCD的边AB，BC，AD上，AE= $\text{[math]}$ AB，CF= $\text{[math]}$ CB，AG= $\text{[math]}$ AD．已知△EFG的面积等于6，则菱形ABCD的面积等于．

查看解析收藏纠错

+选题

二、选择题

13. 0.000182用科学记数法表示应为（）

A . 0182×10^﹣³ B . 1.82×10^﹣⁴ C . 1.82×10^﹣⁵ D . 18.2×10^﹣⁴

查看解析收藏纠错

+选题
14. 如图是由3个大小相同的小正方体组成的几何体，它的左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
15. 小明将如图所示的转盘分成n（n是正整数）个扇形，并使得各个扇形的面积都相等，然后他在这些扇形区域内分别标注连续偶数数字2，4，6，…，2n（每个区域内标注1个数字，且各区域内标注的数字互不相同），转动转盘1次，当转盘停止转动时，若事件“指针所落区域标注的数字大于8”的概率是 $\text{[math]}$ ，则n的取值为（）

A . 36 B . 30 C . 24 D . 18

查看解析收藏纠错

+选题
16. 甲、乙两地相距80km，一辆汽车上午9：00从甲地出发驶往乙地，匀速行驶了一半的路程后将速度提高了20km/h，并继续匀速行驶至乙地，汽车行驶的路程y（km）与时间x（h）之间的函数关系如图所示，该车到达乙地的时间是当天上午（）

A . 10：35 B . 10：40 C . 10：45 D . 10：50

查看解析收藏纠错

+选题
17. 如图，一次函数y=2x与反比例函数y= $\text{[math]}$ （k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为 $\text{[math]}$ ，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

三、解答题

18.

（1）计算：2^﹣¹+（2018﹣π）⁰﹣sin30°；

（2）化简：（a+1）²﹣a（a+1）﹣1．

查看解析收藏纠错

+选题
19.

（1）解方程： $\text{[math]}$ = $\text{[math]}$ +1；

（2）解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
20. 如图，数轴上的点A，B，C，D表示的数分别为﹣3，﹣1，1，2，从A，B，C，D四点中任意取两点，求所取两点之间的距离为2的概率．

查看解析收藏纠错

+选题
21. 小李读一本名著，星期六读了36页，第二天读了剩余部分的 $\text{[math]}$ ，这两天共读了整本书的 $\text{[math]}$ ，这本名著共有多少页？

查看解析收藏纠错

+选题
22. 如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．

（1）求证：△ABE≌△ACF；

（2）若∠BAE=30°，则∠ADC=°．

查看解析收藏纠错

+选题
23. 某班50名学生的身高如下（单位：cm）：
160 163 152 161 167 154 158 171 156 168
178 151 156 154 165 160 168 155 162 173
158 167 157 153 164 172 153 159 154 155
169 163 158 150 177 155 166 161 159 164
171 154 157 165 152 167 157 162 155 160

（1）小丽用简单随机抽样的方法从这50个数据中抽取一个容量为5的样本：161，155，174，163，152，请你计算小丽所抽取的这个样本的平均数；

（2）小丽将这50个数据按身高相差4cm分组，并制作了如下的表格：
身高
频数
频率
147.5～151.5

0.06
151.5～155.5

155.5～159.5
11
m
159.5～163.5

0.18
163.5～167.5
8
0.16
167.5～171.5
4

171.5～175.5
n
0.06
175.5～179.5
2

合计
50
1
①m=，n=；
②这50名学生身高的中位数落在哪个身高段内？身高在哪一段的学生数最多？

查看解析收藏纠错

+选题
24. 如图，校园内有两幢高度相同的教学楼AB，CD，大楼的底部B，D在同一平面上，两幢楼之间的距离BD长为24米，小明在点E（B，E，D在一条直线上）处测得教学楼AB顶部的仰角为45°，然后沿EB方向前进8米到达点G处，测得教学楼CD顶部的仰角为30°．已知小明的两个观测点F，H距离地面的高度均为1.6米，求教学楼AB的高度AB长．（精确到0.1米）参考值： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73．

查看解析收藏纠错

+选题
25. 如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分．

（1）求一次函数y=kx+b（k≠0）的表达式；

（2）若△ACE的面积为11，求点E的坐标；

（3）当∠CBE=∠ABO时，点E的坐标为．

查看解析收藏纠错

+选题
26. 如图1，平行四边形ABCD中，AB⊥AC，AB=6，AD=10，点P在边AD上运动，以P为圆心，PA为半径的⊙P与对角线AC交于A，E两点．

（1）如图2，当⊙P与边CD相切于点F时，求AP的长；

（2）不难发现，当⊙P与边CD相切时，⊙P与平行四边形ABCD的边有三个公共点，随着AP的变化，⊙P与平行四边形ABCD的边的公共点的个数也在变化，若公共点的个数为4，直接写出相对应的AP的值的取值范围．

查看解析收藏纠错

+选题
27. 如图

（1）如图1，将矩形ABCD折叠，使BC落在对角线BD上，折痕为BE，点C落在点C′处，若∠ADB=46°，则∠DBE的度数为°．

（2）小明手中有一张矩形纸片ABCD，AB=4，AD=9．
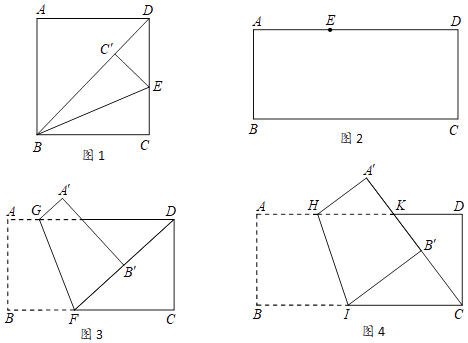
（画一画）
如图2，点E在这张矩形纸片的边AD上，将纸片折叠，使AB落在CE所在直线上，折痕设为MN（点M，N分别在边AD，BC上），利用直尺和圆规画出折痕MN（不写作法，保留作图痕迹，并用黑色水笔把线段描清楚）；
（算一算）
如图3，点F在这张矩形纸片的边BC上，将纸片折叠，使FB落在射线FD上，折痕为GF，点A，B分别落在点A′，B′处，若AG= $\text{[math]}$ ，求B′D的长；
（验一验）
如图4，点K在这张矩形纸片的边AD上，DK=3，将纸片折叠，使AB落在CK所在直线上，折痕为HI，点A，B分别落在点A′，B′处，小明认为B′I所在直线恰好经过点D，他的判断是否正确，请说明理由．

查看解析收藏纠错

+选题
28. 如图，二次函数y=x²﹣3x的图象经过O（0，0），A（4，4），B（3，0）三点，以点O为位似中心，在y轴的右侧将△OAB按相似比2：1放大，得到△OA′B′，二次函数y=ax²+bx+c（a≠0）的图象经过O，A′，B′三点．

（1）画出△OA′B′，试求二次函数y=ax²+bx+c（a≠0）的表达式；

（2）点P（m，n）在二次函数y=x²﹣3x的图象上，m≠0，直线OP与二次函数y=ax²+bx+c（a≠0）的图象交于点Q（异于点O）．
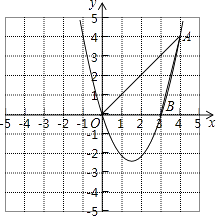
①连接AP，若2AP＞OQ，求m的取值范围；

（3） ②当点Q在第一象限内，过点Q作QQ′平行于x轴，与二次函数y=ax²+bx+c（a≠0）的图象交于另一点Q′，与二次函数y=x²﹣3x的图象交于点M，N（M在N的左侧），直线OQ′与二次函数y=x²﹣3x的图象交于点P′．△Q′P′M∽△QB′N，则线段 NQ的长度等于．

查看解析收藏纠错

+选题

身高	频数	频率
147.5～151.5		0.06
151.5～155.5
155.5～159.5	11	m
159.5～163.5		0.18
163.5～167.5	8	0.16
167.5～171.5	4
171.5～175.5	n	0.06
175.5～179.5	2
合计	50	1

江苏省镇江市2018年中考数学试卷

一、填空题

二、选择题

三、解答题

相关试卷 收起∨

相关试卷收起∨