山东省德州市2018年中考数学试卷

修改时间：2024-07-13 浏览次数：886 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 3的相反数是（）

A . 3 B . $\text{[math]}$ C . -3 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列图形中，既是轴对称又是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 一年之中地球与太阳之间的距离随时间而变化，1个天文单位是地球与太阳之间的平均距离，即1.496亿 $\text{[math]}$ ．用科学记数法表示1.496亿是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 已知一组数据：6，2，8， $\text{[math]}$ ，7，它们的平均数是6．则这组数据的中位数是（）

A . 7 B . 6 C . 5 D . 4

查看解析收藏纠错

+选题
6. 如图，将一副三角尺按不同的位置摆放，下列摆放方式中 $\text{[math]}$ 与 $\text{[math]}$ 互余的是（）

A . 图① B . 图② C . 图③ D . 图④

查看解析收藏纠错

+选题
7. 如图，函数 $\text{[math]}$ 和 $\text{[math]}$ ( $\text{[math]}$ 是常数，且 $\text{[math]}$ )在同一平面直角坐标系的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 分式方程 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无解

查看解析收藏纠错

+选题
9. 如图，从一块直径为 $\text{[math]}$ 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 给出下列函数：①y=﹣3x+2；②y= $\text{[math]}$ ；③y=2x²；④y=3x，上述函数中符合条作“当x＞1时，函数值y随自变量x增大而增大“的是（）

A . ①③ B . ③④ C . ②④ D . ②③

查看解析收藏纠错

+选题
11. 我国南宋数学家杨辉所著的《详解九章算术》一书中，用下图的三角形解释二项式
$\text{[math]}$ 的展开式的各项系数，此三角形称为“杨辉三角”．
根据“杨辉三角”请计算 $\text{[math]}$ 的展开式中从左起第四项的系数为（）

A . 84 B . 56 C . 35 D . 28

查看解析收藏纠错

+选题
12. 如图，等边三角形 $\text{[math]}$ 的边长为4，点 $\text{[math]}$ 是△ $\text{[math]}$ 的中心， $\text{[math]}$ .绕点 $\text{[math]}$ 旋转 $\text{[math]}$ ，分别交线段 $\text{[math]}$ 于D、E两点，连接 $\text{[math]}$ ，给出下列四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③四边形 $\text{[math]}$ 的面积始终等于 $\text{[math]}$ ；④△ $\text{[math]}$ 周长的最小值为6，上述结论中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

13. 计算： $\text{[math]}$ =．

查看解析收藏纠错

+选题
14. 若 x₁、x₂是一元二次方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ =．

查看解析收藏纠错

+选题
15. 如图， $\text{[math]}$ 为 $\text{[math]}$ 的平分线. $\text{[math]}$ ， $\text{[math]}$ . $\text{[math]}$ .则点 $\text{[math]}$ 到射线 $\text{[math]}$ 的距离为．

查看解析收藏纠错

+选题
16. 如图。在 $\text{[math]}$ 的正方形方格图形中，小正方形的顶点称为格点. $\text{[math]}$ 的顶点都在格点上，则 $\text{[math]}$ 的正弦值是．

查看解析收藏纠错

+选题
17. 对于实数a，b，定义运算“◆”：a◆b= $\text{[math]}$ ，例如4◆3，因为4＞3．所以4◆3= $\text{[math]}$ =5．若x，y满足方程组 $\text{[math]}$ ，则x◆y=.

查看解析收藏纠错

+选题
18. 如图，反比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 在第三象限交于点 $\text{[math]}$ .点 $\text{[math]}$ 的坐标为(一3，0)，点 $\text{[math]}$ 是 $\text{[math]}$ 轴左侧的一点.若以 $\text{[math]}$ 为顶点的四边形为平行四边形.则点 $\text{[math]}$ 的坐标为.

查看解析收藏纠错

+选题

三、解答题

19. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 是不等式组 $\text{[math]}$ 的整数解.

查看解析收藏纠错

+选题
20. 某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲)，从全校学生中随机抽取部分学生进行问卷调查，并把调查结果绘制成两幅不完整的统计图.
请根据以上信息，解答下列问题：

（1）这次被调查的学生共有多少人?

（2）请将条形统计图补充完整；

（3）若该校约有1500名学生，估计全校学生中喜欢娱乐节目的有多少人?

（4）该校广播站需要广播员，现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名，求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)

查看解析收藏纠错

+选题
21. 如图，两座建筑物的水平距离 $\text{[math]}$ 为 $\text{[math]}$ .从 $\text{[math]}$ 点测得 $\text{[math]}$ 点的仰角 $\text{[math]}$ 为53° ，从 $\text{[math]}$ 点测得 $\text{[math]}$ 点的俯角 $\text{[math]}$ 为37° ，求两座建筑物的高度(参考数据： $\text{[math]}$

查看解析收藏纠错

+选题
22. 如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E．点C是弧BF的中点．

（1）求证：AD⊥CD；

（2）若∠CAD=30°．⊙O的半径为3，一只蚂蚁从点B出发，沿着BE--EC--弧CB爬回至点B，求蚂蚁爬过的路程(π≈3.14， $\text{[math]}$ ≈1.73，结果保留一位小数．)

查看解析收藏纠错

+选题
23. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台.假定该设备的年销售量y(单位：台)和销售单价 $\text{[math]}$ (单位：万元)成一次函数关系.

（1）求年销售量 $\text{[math]}$ 与销售单价 $\text{[math]}$ 的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?

查看解析收藏纠错

+选题
24. 再读教材：
宽与长的比是 $\text{[math]}$ (约为0.618)的矩形叫做黄金矩形，黄金矩形给我们以协调，匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果，都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.(提示； $\text{[math]}$ )
第一步，在矩形纸片一端.利用图①的方法折出一个正方形，然后把纸片展平.
第二步，如图②.把这个正方形折成两个相等的矩形，再把纸片展平.
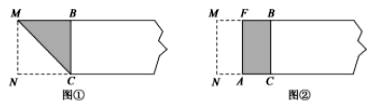
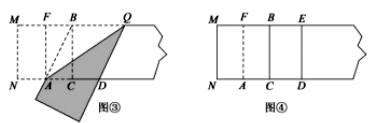
第三步，折出内侧矩形的对角线 $\text{[math]}$ ，并把 $\text{[math]}$ 折到图③中所示的 $\text{[math]}$ 处，
第四步，展平纸片，按照所得的点 $\text{[math]}$ 折出 $\text{[math]}$ ，使 $\text{[math]}$ ，则图④中就会出现黄金矩形，
问题解决：

（1）图③中 $\text{[math]}$ =(保留根号)；

（2）如图③，判断四边形 $\text{[math]}$ 的形状，并说明理由；

（3）请写出图④中所有的黄金矩形，并选择其中一个说明理由.

（4）结合图④.请在矩形 $\text{[math]}$ 中添加一条线段，设计一个新的黄金矩形，用字母表示出来，并写出它的长和宽.

查看解析收藏纠错

+选题
25. 如图1，在平面直角坐标系中，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，其中 $\text{[math]}$ ， $\text{[math]}$ .该抛物线与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于另一点 $\text{[math]}$ .

（1）求 $\text{[math]}$ 的值及该抛物线的解析式；

（2）如图2.若点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的一动点(不与 $\text{[math]}$ 重合).分别以 $\text{[math]}$ 、 $\text{[math]}$ 为斜边，在直线 $\text{[math]}$ 的同侧作等腰直角△ $\text{[math]}$ 和等腰直角△ $\text{[math]}$ ，连接 $\text{[math]}$ ，试确定△ $\text{[math]}$ 面积最大时 $\text{[math]}$ 点的坐标.

（3）如图3.连接 $\text{[math]}$ 、 $\text{[math]}$ ，在线段 $\text{[math]}$ 上是否存在点 $\text{[math]}$ ，使得以 $\text{[math]}$ 为顶点的三角形与△ $\text{[math]}$ 相似，若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题

山东省德州市2018年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨