修改时间:2023-11-27 浏览次数:43 类型:同步测试
数学课上,老师提出了如下问题:
已知点在直线
上,
, 在同一平面内,过点
作射线
, 满足
当
时,如图1所示,求
的度数.
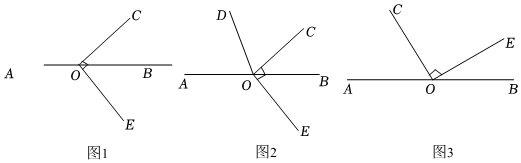
甲同学:以下是我的解答过程部分空缺
解:如图2,点
在直线
上,
.
,
▲
,
平分
.
▲
,
,
▲
乙同学:“我认为还有一种情况.”
请完成以下问题:
试题篮