（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（培优卷）

1. 有理数 $\text{[math]}$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
2. 四个各不相等的整数 $\text{[math]}$ ，满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 0 B . 4 C . 10 D . 无法确定

查看解析收藏纠错

+选题
3. 已知 $\text{[math]}$ ，则式子： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
4. 有理数a、b满足|a－b|=|a|+| b|，则a、b应满足的条件是（）

A . ab≥0 B . ab ＞1 C . ab ≤0 D . ab≤1

查看解析收藏纠错

+选题
5. 有理数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）

① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .

A . 4个 B . 3个 C . 2个 D . 1个

查看解析收藏纠错

+选题
6. 九宫格起源于中国古代的神秘图案河图和洛书.如图，将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 若abc≠0，则 $\text{[math]}$ ＋ $\text{[math]}$ + $\text{[math]}$ 的值为（）

A . ±3或±1 B . ±3或0或±1 C . ±3或0 D . 0或±1

查看解析收藏纠错

+选题
8. 若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1或－3 B . －1或－3 C . ±1或±3 D . 无法判断

查看解析收藏纠错

+选题
9. 下列说法正确的有（）
① $\text{[math]}$ ,则 $\text{[math]}$ ；②数轴上到某点距离相等的两个点对应的数相等

③ $\text{[math]}$ ,则 $\text{[math]}$ ；④ $\text{[math]}$ 则 $\text{[math]}$

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
10. 如果有4个不同的正整数 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ，那么 $\text{[math]}$ 的值为（）

A . 0 B . 9 C . 8076 D . 8090

查看解析收藏纠错

+选题

11. 若n＝ $\text{[math]}$ ， abc＜0，则n的值为．

查看解析收藏纠错

+选题
12. 三个有理数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．当 $\text{[math]}$ 时， $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
13. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：
十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如，十进制中16+10=26，用十六进制表示为10+A=1A；十进制中25-15=10，用十六进制表示为19−F=A．由上可知，在十六进制中B×D=（运算结果用十六进制表示）．

查看解析收藏纠错

+选题
14. 若a，b，c都不为0，则 $\text{[math]}$ 的值可能是．

查看解析收藏纠错

+选题
15. 已知abc≠0，且 $\text{[math]}$ 的最大值为m，最小值为n，则m+n＝.

查看解析收藏纠错

+选题

16. 已知三个有理数a，b，c的积是负数，它们的和是正数，当x= $\text{[math]}$ 时，求代数式： x²⁰¹⁹-2x+2的值.

查看解析收藏纠错

+选题
17. 有一种“算24”的游戏，其规则是：任取四个1～13之间的自然数，将这四个数（每数只能用一次）进行加减乘除混合运算，其结果为24.例如2，3，4，5作运算.（5+3－2）×4=24，现有四个有理数3、4、－6、10，运用以上规则写出等于24的算式，你能写出几种算法?

查看解析收藏纠错

+选题
18. 阅读下列内容，并完成相关问题：
小明说：“我定义了一种新的运算，叫❈（加乘）运算．”然后他写出了一些按照❈（加乘）运算的运算法则进行运算的算式：
（+4）❈（+2）=+6；（﹣4）❈（﹣3）=+7；
（﹣5）❈（+3）=﹣8；（+6）❈（﹣7）=﹣13；
（+8）❈0=8；0❈（﹣9）=9．
小亮看了这些算式后说：“我知道你定义的❈（加乘）运算的运算法则了．”
聪明的你也明白了吗？

（1）归纳❈（加乘）运算的运算法则：
两数进行❈（加乘）运算时，．
特别地，0和任何数进行❈（加乘）运算，或任何数和0进行❈（加乘）运算，．

（2）计算：[（﹣2）❈（+3）]❈[（﹣12）❈0]（括号的作用与它在有理数运算中的作用一致）

（3）我们知道加法有交换律和结合律，这两种运算律在有理数的❈（加乘）运算中还适用吗？请你任选一个运算律，判断它在❈（加乘）运算中是否适用，并举例验证．（举一个例子即可）”

查看解析收藏纠错

+选题
19. 已知： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题

20.

（1）已知 $\text{[math]}$ 互为相反数， $\text{[math]}$ 互为倒数， $\text{[math]}$ 的绝对值是2，求 $\text{[math]}$ 的值；

（2）若 $\text{[math]}$ 在数轴上的位置如图所示，化简式子： $\text{[math]}$ 。

查看解析收藏纠错

+选题
21. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答问题.
（提出问题）三个有理数a，b，c满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

（解决问题）解：由题意，得a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①a，b，c都是正数，即 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 时，则 $\text{[math]}$ ；

②当a，b，c中有一个为正数，另两个为负数时，不妨设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ，综上所述， $\text{[math]}$ 值为3或−1.

（探究）请根据上面的解题思路解答下面的问题：

（1）三个有理数a，b，c满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

（2）若a，b，c为三个不为0的有理数，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
22. 有个补充运算符号的游戏：在“1□2□ $\text{[math]}$ □9”中的每个□内，填入+、-、×、÷中的某一个（可重复使用），然后计算结果．

（1）计算： $\text{[math]}$ （直接写出结果）；

（2）若 $\text{[math]}$ □ $\text{[math]}$ ，请推算□内的符号应是什么？

（3）请在□内填上×、÷中的一个，使计算更加简便，然后计算 $\text{[math]}$ □ $\text{[math]}$

查看解析收藏纠错

+选题
23. 概念学习：
现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2写作2^③ ，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）写作（﹣3）^④ ，读作“（﹣3）的圈4次方”，一般地把 $\text{[math]}$ （a≠0）写作a^ⓝ ，读作“a的圈n次方”．

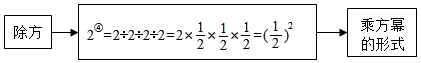
初步探究：

（1）直接写出计算结果：3^②＝；（﹣ $\text{[math]}$ ）^③＝；

（2）下列关于除方说法中，错误的有
A．任何非零数的圈2次方都等于1

B．任何非零数的圈3次方都等于它的倒数

C．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数

D．圈n次方等于它本身的数是1或﹣1．
深入思考：我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？

（3）
比较：（﹣2）^⑩（﹣4）^⑩；（填“＞”“＜”或“＝”）

（4）计算：﹣1^⑥+4²÷（﹣ $\text{[math]}$ ）^④×（﹣7）^③ ．

查看解析收藏纠错

+选题

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

（人教版）2023-2024学年七年级数学上册1.4 有理数的乘除法同步分层训练（培优卷）

相关试卷收起∨