浙江省宁波市江北区2020年数学中考模拟试卷（5月）

1. 下列防疫的图标中是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 计算2a²+a² ，结果正确的是（　　）

A . 2a⁴ B . 2a² C . 3a⁴ D . 3a²

查看解析收藏纠错

+选题
3. 下列几何体中，主视图不是矩形的几何体是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 2020年4月24日，国家航天局在中国航天日线上启动仪式上公布：中国行星探测任务被命名为“天问系列”，首次火星探测任务被命名为“天问一号”.火星是与地球形貌最接近的大行星，火星也是我们的近邻，最近的时候距离地球约5500万千米.其中“5500万千米”用科学记数法表示为（）

A . 550×10⁸（米） B . 55×10⁹（米） C . 5.5×10¹⁰（米） D . 0.55×10¹¹（米）

查看解析收藏纠错

+选题
5. 如图，在数轴上表示不等式组 $\text{[math]}$ 的解集，其中正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 一组数据1，1，1，3，5，9，17，若加入一个整数a，一定不会发生变化的统计量是（）

A . 平均数 B . 中位数 C . 方差 D . 众数

查看解析收藏纠错

+选题
7. 下列命题中，逆命题为真命题的是（）

A . 实数a、b，若a=b，则|a|=|b| B . 两直线平行，同位角相等 C . 对顶角相等 D . 若ac²＞bc² ，则a＞b

查看解析收藏纠错

+选题
8. 在高速公路上，从3千米处开始，每隔4千米设置一个限速标志牌，而且从10千米处开始，每隔9千米设置一个速度监控仪，刚好在19千米处同时经过这两种标志.则第三次同时经过这两种标志的地点的千米数为（）

A . 32 B . 55 C . 91 D . 127

查看解析收藏纠错

+选题
9. 如图，以Rt△ABC各边为边分别向外作等边三角形，编号为①、②、③，将②、①如图所示依次叠在③上，已知四边形EMNC与四边形MPQN的面积分别为9 $\text{[math]}$ 与7 $\text{[math]}$ ，则斜边BC的长为（）

A . 5 B . 9 C . 10 D . 16

查看解析收藏纠错

+选题
10. 如图，Rt△ACB中，∠C=90°，AC=6，BC=8，半径为1的⊙O与AC，BC相切，当⊙O沿边CB平移至与AB相切时，则⊙O平移的距离为（）

A . 3 B . 4 C . 5 D . 6

查看解析收藏纠错

+选题

11. 8的立方根为.

查看解析收藏纠错

+选题
12. 因式分解：x²﹣1＝.

查看解析收藏纠错

+选题
13. 若二次根式 $\text{[math]}$ 有意义，则x的取值范围是

查看解析收藏纠错

+选题
14. 如图，两直线l₁∥1₂ ，等腰直角三角尺ABC的两个锐角顶点A，B分别在l₁∥1₂上，若∠1=75°，则∠2=.

查看解析收藏纠错

+选题
15. 如图，点A是反比例函数y= $\text{[math]}$ 图象在第一象限上的一点，连结AO并延长交图象的另一分支于点B，延长BA至点C，过点C作CD⊥x轴，垂足为D，交反比例函数图象于点E.若 $\text{[math]}$ ，△BDC的面积为6，则k=.

查看解析收藏纠错

+选题
16. 已知等腰直角△ABC，∠C=90°，AC=2，D为边AC上一动点，连结BD，在射线BD上取一点E使BE•BD=AB².若点D由A运动到C，则点E运动的路径长为.

查看解析收藏纠错

+选题

17.

（1）计算：（2020﹣π）⁰﹣ $\text{[math]}$ +|﹣3 $\text{[math]}$ |；

（2）解方程： $\text{[math]}$ .

查看解析收藏纠错

+选题
18. “天空之城”摩天轮，位于宁波市杭州湾新区欢乐世界.摩天轮高约126米（最高点到地面的距离）.如图，点O是摩天轮的圆心，AB是其垂直于地面的直径，小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°，测得圆心O的仰角为30°，求摩天轮的半径.（结果保留根号）

查看解析收藏纠错

+选题
19. 2020年伊始，一场突如其来的疫情防控战在中华大地骤然打响，全国人民自觉居家减少外出，师生停课不停学，举国共抗疫情.某中学在复学后，为了了解学生们在居家期间的生活状态，以更好地保护复学后学生们的身心健康，对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为：（A）强身健体、（B）艺术熏陶、（C）经典阅读、（D）分担劳动、（E）其他.针对以上活动种类，统计学生们花时间最多的种类的人数，以绘制成如下两幅不完整的条形统计图和扇形统计图.

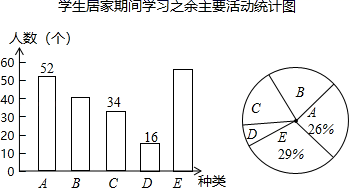
请根据图中的信息，回答下列问题.

（1）被抽样调查的总人数为人；

（2）补全条形统计图；

（3）若该校共有学生1800人，请估算种类D的大约人数；

（4）据此疫情经历，给自己提出一条人生建议.

查看解析收藏纠错

+选题
20. 矩形ABCD，AB=6，BC=8，四边形EFGH的顶点E、G在矩形的边AD、BC上；顶点F、H在矩形的对角线BD上.

（1）如图1，当四边形EFGH是平行四边形时，求证：△DEH≌△BGF.

（2）如图2，当四边形EFGH是正方形时，求BF的长.

查看解析收藏纠错

+选题
21. 随着宁波市江北区慈城古县城旅游开发的推进，到慈城旅游的全国各地游客逐年上升.深受当地老百姓喜爱的两种本土特产杨梅和年糕，也深受外地游客的青睐.现在，有两种特产大礼包的组合是这样的：若购买2筐杨梅和3盒年糕，则需花费270元；若购买1筐杨梅和4盒年糕，则需花费260元.（杨梅、年糕分别按包装筐和包装盒计价）

（1）求一筐杨梅、一盒年糕的售价分别是多少元？

（2）如果需购买两种特产共12件（1筐或1盒称为1件），要求年糕的盒数不高于杨梅筐数的两倍，请你设计一种购买方案，使所需总费用最低.

查看解析收藏纠错

+选题
22. 将立方体纸盒沿某些棱剪开，且使六个面连在一起，然后铺平，可以得到其表面展开图的平面图形.

（1）以下两个方格图中的阴影部分能表示立方体表面展开图的是（填A或B）.

（2）在以下方格图中，画一个与（1）中呈现的阴影部分不相似（包括不全等）的立方体表面展开图.（用阴影表示）

（3）如图中的实线是立方体纸盒的剪裁线，请将其表面展开图画在右图的方格图中.（用阴影表示）

查看解析收藏纠错

+选题

23. 一般地，对于已知一次函数y₁=ax+b，y₂=cx+d（其中a，b，c，d为常数，且ac＜0），定义一个新函数y= $\text{[math]}$ ，称y是y₁与y₂的算术中项，y是x的算术中项函数.

（1）如：一次函数y₁= $\text{[math]}$ x﹣4，y₂=﹣ $\text{[math]}$ x+6，y是x的算术中项函数，即y= $\text{[math]}$ .

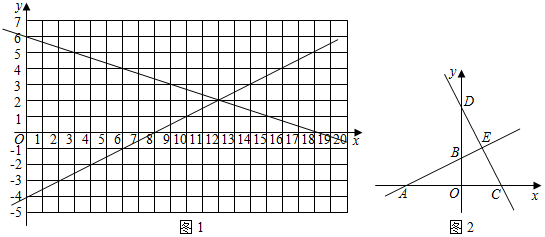
①自变量x的取值范围是，当x=时，y有最大值；

②根据函数研究的途径与方法，请填写下表，并在图1中描点、连线，画出此函数的大致图象；

x	8	9	10	12	13	14	16	17	18
y	0	1.2	1.6		2.04	2		1.2	0

③请写出一条此函数可能有的性质；

（2）如图2，已知一次函数y₁= $\text{[math]}$ x+2，y₂=﹣2x+6的图象交于点E，两个函数分别与x轴交于点A，C，与y轴交于点B，D，y是x的算术中项函数，即y= $\text{[math]}$ .

①判断：点A、C、E是否在此算术中项函数的图象上；

②在平面直角坐标系中是否存在一点，到此算术中项函数图象上所有点的距离相等，如果存在，请求出这个点；如果不存在，请说明理由.

查看解析收藏纠错

+选题

24. 如图1，平面直角坐标系中，△OAB的边OA在x轴的正半轴上，点B在第二象限，且∠AOB=135°，OA=2，OB=2 $\text{[math]}$ ，抛物线y=﹣ $\text{[math]}$ x²+bx+c经过点B，并与y轴交于点C（0，5），点P在抛物线的对称轴上.

（1）求b、c的值，及抛物线的对称轴.

（2）求证：以点M（2，5）为圆心，半径为2 $\text{[math]}$ 的圆与边AB相切.

（3）若满足条件∠AOB+∠POD=180°与OB：OD=OA：OP的点D恰好在抛物线上，请求出此时点P的坐标.

查看解析收藏纠错

+选题

浙江省宁波市江北区2020年数学中考模拟试卷（5月）

一、选择题

二、填空题

三、解答题

相关试卷收起∨

浙江省宁波市江北区2020年数学中考模拟试卷（5月）

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨