题型:综合题 题类:模拟题 难易度:困难
江苏省扬州市树人中学2020年数学中考二模试卷
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
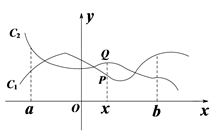
|
滑行时间t1/s |
0 |
1 |
2 |
3 |
4 |
|
滑行距离y1/s |
0 |
4.5 |
14 |
28.5 |
48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22 , 滑雪者从A出发在缓冲带BC上停止,一共用了23s.

试题篮