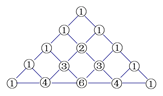
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是

,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了


的展开式(按

的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的

个数

,恰好对应着

展开式中的各项系数,第四行的

个数

,恰好对应着

展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题: