2017-2018学年浙教版八年级上学期数学期末模拟试卷

1. 下列曲线中不能表示y与x的函数的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 在平面直角坐标系中，若点A（a，﹣b）在第一象限内，则点B（a，b）所在的象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

查看解析收藏纠错

+选题
3. 若a>b，则下列各式中一定成立的是（）

A . ma>mb B . a²>b² C . 1－a>1－b D . b－a<0

查看解析收藏纠错

+选题
4. 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（　　）

A . 4 B . 6 C . 8 D . 10

查看解析收藏纠错

+选题
6. 如图：AB=A′B′，∠A=∠A′，若△ABC≌△A′B′C′，则还需添加的一个条件有（）种．

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
7. 如图，在△ABC中，∠A=52°，∠ABC与∠ACB的角平分线交于D₁ ， ∠ABD₁与∠ACD₁的角平分线交于点D₂ ，依此类推，∠ABD₄与∠ACD₄的角平分线交于点D₅ ，则∠BD₅C的度数是（）

A . 56° B . 60° C . 68° D . 94°

查看解析收藏纠错

+选题
8. 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和BC′F的周长之和为（）

A . 3 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
9. 如图，直线y₁=x+b与y₂=kx﹣1相交于点P，点P的横坐标为﹣1，则关于x的不等式x+b＞kx﹣1的解集在数轴上表示正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题

10. 写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题：．

查看解析收藏纠错

+选题
11. 已知点P的坐标为（5，﹣12），则点P到x轴的距离为．

查看解析收藏纠错

+选题
12. 如果一次函数y=（m﹣3）x+m﹣2的图象一定经过第三、第四象限，那么常数m的取值范围为．

查看解析收藏纠错

+选题
13. 如图，已知△ABC，BC=10，BC边的垂直平分线交AB，BC于点E、D．若△ACE的周长为12，则△ABC的周长为．

查看解析收藏纠错

+选题
14. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1））．图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃ ．若正方形EFGH的边长为2，则S₁+S₂+S₃=．

查看解析收藏纠错

+选题
15. 在等腰△ABC中，AD⊥BC交直线BC于点D，若AD= $\text{[math]}$ BC，则△ABC的顶角的度数为．

查看解析收藏纠错

+选题

16. 解不等式组 $\text{[math]}$ ．

查看解析收藏纠错

+选题

17. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣1，﹣1），B（﹣3，3），C（﹣4，1）

①画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出点B的对应点B₁的坐标；
②画出△ABC向下平移3个单位的△A₂B₂C₂ ，并写出点C的对应点C₂的坐标．

查看解析收藏纠错

+选题

18. 如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．

（1）求证：AD=AE；

（2）连接OA，BC，试判断直线OA，BC的关系并说明理由．

查看解析收藏纠错

+选题
19. 紫薇花园住宅小区计划购买并栽种甲、乙两种树苗共280株．已知甲种树苗每株60元，乙种树苗每株90元．

（1）若购买树苗共用21000元，则甲乙两种树苗应各买多少株？

（2）设购买这两种树苗共用y元，求y（元）与甲种树苗x（株）之间的函数关系式．

（3）据统计，甲乙两种树苗每株对空气的净化指数分别为0.2和0.6，如何购买甲乙两种树苗才能保证该小区的空气净化指数之和不低于88而且费用最低？并请你求出最低费用的是多少元？

查看解析收藏纠错

+选题
20. 动手操作题：如何能把一个三角形分成两个等腰三角形吗？
实际上，一个三角形只要具备下列三个条件之一，都可以被分成两个等腰三角形：
①一个角为90°；②一个角是另一个的2倍（第三角必须大于45°）；
③一个角是另一个角的3倍.今天，我们通过作图来验证这个结论。

（1）
问题1：
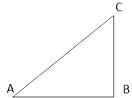
如图，Rt△ABC中，求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC
边上的交点D的位置.

（2）
问题2：
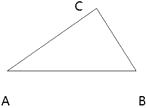
如图，△ABC中，∠ACB=80°， ∠BAC=40°，求画一条直线l把△ABC分成两个等腰三角形，并在图中标注两个顶角的度数.

（3）
问题3：
如图，△ABC中，∠ACB=120°， ∠BAC=40°，求画一条直线l把△ABC分成两个等腰三角形，并在图中标注两个顶角的度数.

（4）问题：4：
如果等腰三角形能被一条直线分成两个等腰三角形，则原等腰三角形的顶角可以是°.（至少写出三个）

（5）拓展：已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（）

A . 6条 B . 7条 C . 8条 D . 9条

查看解析收藏纠错

+选题
21. 已知，直线 $\text{[math]}$ 与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°．且点P（1，a）为坐标系中的一个动点．

（1）求三角形ABC的面积S_△_ABC；

（2）请说明不论a取任何实数，三角形BOP的面积是一个常数；

（3）要使得△ABC和△ABP的面积相等，求实数a的值．

查看解析收藏纠错

+选题
22. “五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．

（1）求a的值．

（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．

（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

查看解析收藏纠错

+选题

2017-2018学年浙教版八年级上学期数学期末模拟试卷

一、单选题

二、填空题

三、计算题

四、作图题

五、综合题

相关试卷收起∨

2017-2018学年浙教版八年级上学期数学期末模拟试卷

一、单选题

二、填空题

三、计算题

四、作图题

五、综合题

相关试卷 收起∨

相关试卷收起∨