【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略2 二次函数的应用

1. 关于二次函数y=-（x-3）²+2的最值，下列说法正确的是（）

A . 有最大值3 B . 有最小值3 C . 有最大值2 D . 有最小值2

查看解析收藏纠错

+选题
2. 观察下面的表格，一元二次方程 $\text{[math]}$ 的一个近似解是（）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 二次函数y＝ax²-2ax+c（a≠0）的图象过点（3，0），方程ax²-2ax+c＝0的解为（）

A . x₁＝-3，x₂＝-1 B . x₁＝-1，x₂＝3 C . x₁＝1，x₂＝3 D . x₁＝-3，x₂＝1

查看解析收藏纠错

+选题
4. 现有一根长为50cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm ² ，一边长为xcm，则y与x之间的函数表达式为（）

A . y=x(50-x) B . y=x(50-2x) C . y=x(25-2x) D . y=x(25-x)

查看解析收藏纠错

+选题
5. 已知抛物线 $\text{[math]}$ 与x轴有两个不同的交点，则关于x的一元二次方程 $\text{[math]}$ 根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 实数根 D . 无法确定

查看解析收藏纠错

+选题
6. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）

A . -4<x<3 B . x<-4 C . 3-<<x<-4 D . x>3或x<-4

查看解析收藏纠错

+选题
7. 已知抛物线y=x²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是（）

A . x＜-1 B . -1＜x＜3 C . x＜-1或x＞3 D . x＜-1或x＞4

查看解析收藏纠错

+选题
8. 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，在第四象限抛物线上有一点 $\text{[math]}$ ，若 $\text{[math]}$ 是以 $\text{[math]}$ 为底边的等腰三角形，则点 $\text{[math]}$ 的横坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
9. “抖音直播带货”已经成为一种热门的销售方式，某抖音主播代销某一品牌的电子产品（这里代销指厂家先免费提供货源，待货物销售后再进行结算，未售出的由厂家负责处理）．销售中发现每件售价99元时，日销售量为200件，当每件电子产品每下降5元时，日销售量会增加10件．已知每售出1件电子产品，该主播需支付厂家和其他费用共50元，设每件电子产品售价为x（元），主播每天的利润为w（元），则w与x之间的函数解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，已知抛物线经过点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴交于点 $\text{[math]}$ ， P为AC上的一个动点，则有以下结论：①抛物线的对称轴为直线 $\text{[math]}$ ；②抛物线的最大值为 $\text{[math]}$ ；③ $\text{[math]}$ ；④OP的最小值为 $\text{[math]}$ ．则正确的结论为（）

A . ①②④ B . ①② C . ①②③ D . ①③④

查看解析收藏纠错

+选题

11. 某工厂今年八月份医用防护服的产量是50万件，计划九月份和十月份增加产量，如果月平均增长率为x，那么十月份医用防护服的产量y（万件）与x之间的函数表达式为．

查看解析收藏纠错

+选题
12. 已知二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

查看解析收藏纠错

+选题
13. 某产品每件成本10元，试销阶段每件产品的销售单价x（元/件）与日销售量y（件）之间的关系如下表．
x（元∕件）
15
18
20
22
…
y（件）
250
220
200
180
…
按照这样的规律可得，日销售利润w（元）与销售单价x（元/件）之间的函数关系式是．

查看解析收藏纠错

+选题
14. 要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 $\text{[math]}$ 处达到最高，高度为 $\text{[math]}$ ，水柱落地处离池中心 $\text{[math]}$ ，水管长度应为．

查看解析收藏纠错

+选题
15. 开口向上的抛物线 $\text{[math]}$ 过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个数中有且只有一个数大于零，则a的取值范围是.

查看解析收藏纠错

+选题
16. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒1个单位的速度沿线段 $\text{[math]}$ 运动到点 $\text{[math]}$ 停止，同时动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒4个单位的速度沿折线 $\text{[math]}$ 运动到点 $\text{[math]}$ 停止．图2是点 $\text{[math]}$ 运动时， $\text{[math]}$ 的面积 $\text{[math]}$ 与运动时间 $\text{[math]}$ 函数关系的图象，则 $\text{[math]}$ 的值是．

查看解析收藏纠错

+选题

17. 已知抛物线的对称轴是直线x=2，顶点在直线y=x-1上，并且经过点(3，-8)．

（1）求这条抛物线的函数表达式；

（2）若点(1，y₁)和(4，y₂)都在这条抛物线上，试判断y₁、y₂的大小关系．

查看解析收藏纠错

+选题
18. 已知二次函数y＝x²＋2(m－1)x－2m（m为常数）．

（1）求证无论m为何值，该函数图象与x轴总有两个公共点；

（2）若点A(x₁ ，－1)､B(x₂ ，－1)在该函数图象上，将图像沿直线AB翻折，顶点恰好落在x轴上，求m的值．

查看解析收藏纠错

+选题
19. 用10米的铝合金制成如图窗框矩形ABCD，其中点E，F分别在边AB，CD上，点G，H分别在边EF，BC上，且EF∥BC，GH⊥BC，BE=BC，BE≥3AE，记窗框矩形ABCD的面积为s平方米，边长BC为x米．

（1）求s关于x的表达式及自变量x的取值范围．

（2）求s的最大值．

查看解析收藏纠错

+选题
20. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行，大熊猫是成都最具特色的对外传播标识物和“品牌图腾”，是天府之国享有极高知名度的个性名片．此次成都大运会吉祥物“蓉宝”（如图1）便是以熊猫基地真实的大熊猫“芝麻”为原型创作的．某商店销售“蓉宝”的公仔毛绒玩具，进价为30元/件，经市场调查发现：该商品的月销售量y（件）与销售价x（元/件）之间的关系如图2所示．
图1 图2

（1）求y关于x的函数解析式；

（2）由于某种原因，该商品进价提高了a元/件（ $\text{[math]}$ ），如果规定该玩具售价不超过40元/件，该商品在今后的销售中，月销售量与销售价仍然满足（1）中的函数关系，若该商品的月销售最大利润是2400元，求a的值．

查看解析收藏纠错

+选题
21. $\text{[math]}$ 小明在一次打篮球时，篮球传出后的运动路线为如图所示的抛物线，以小明所站立的位置为原点 $\text{[math]}$ 建立平面直角坐标系，篮球出手时在 $\text{[math]}$ 点正上方 $\text{[math]}$ 处的点 $\text{[math]}$ 已知篮球运动时的高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 之间满足函数表达式 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式；

（2）求篮球在运动的过程中离地面的最大高度；

（3）小亮手举过头顶，跳起后的最大高度为 $\text{[math]}$ ，若小亮要在篮球下落过程中接到球，求小亮离小明的最短距离 $\text{[math]}$ ．

查看解析收藏纠错

+选题
22. 如图，抛物线 $\text{[math]}$ 与坐标轴相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，点D为直线 $\text{[math]}$ 下方抛物线上一动点，过点D作x轴的垂线，垂足为G； $\text{[math]}$ 交直线 $\text{[math]}$ 于点E．

（1）求抛物线的函数表达式；

（2）求 $\text{[math]}$ 的最大值；

（3）过点B的直线 $\text{[math]}$ 交y轴于点C，交直线 $\text{[math]}$ 于点F，H是y轴上一点，当四边形 $\text{[math]}$ 是矩形时，求点H的坐标．

查看解析收藏纠错

+选题
23. 某公园修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安装一个可调节角度的喷水头，从喷水头喷出的水柱形状是一条抛物线．建立如图所示的平面直角坐标系，抛物线形水柱的竖直高度 $\text{[math]}$ （单位：m）与到池中心的水平距离 $\text{[math]}$ （单位：m）满足的关系式近似为 $\text{[math]}$ （ $\text{[math]}$ ）．

（1）在某次安装调试过程中，测得 $\text{[math]}$ 与 $\text{[math]}$ 的部分对应值如下表：
水平距离 $\text{[math]}$
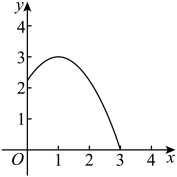
0
0.5
1
1.5
2
2.5
3
竖直高度 $\text{[math]}$
2.25
2.8125
3
2.8125
2.25
1.3125
0
根据表格中的数据，解答下列问题：
①水管的长度是m；
②求出 $\text{[math]}$ 与 $\text{[math]}$ 满足的函数解析式 $\text{[math]}$ （ $\text{[math]}$ ）；

（2）安装工人在上述基础上进行了下面两种调试：
①不改变喷水头的角度，将水管长度增加1m，水柱落地时与池中心的距离为 $\text{[math]}$ ；
②不改变水管的长度，调节喷水头的角度，使得水柱满足 $\text{[math]}$ ，水柱落地时与池中心的距离为 $\text{[math]}$ ．则比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是： $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

查看解析收藏纠错

+选题

【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略2 二次函数的应用

一、选择题

二、填空题

三、解答题

相关试卷收起∨

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

水平距离 $\text{[math]}$	0	0.5	1	1.5	2	2.5	3
竖直高度 $\text{[math]}$	2.25	2.8125	3	2.8125	2.25	1.3125	0

x（元∕件）	15	18	20	22	…
y（件）	250	220	200	180	…

【浙教版】2023-2024学年数学九年级上册期末冲刺满分攻略2 二次函数的应用

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨