2021-2022学年浙教版数学七下1.3平行线的判定同步练习

1. 如图，直线 $\text{[math]}$ 被直线 $\text{[math]}$ 所截下列条件能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，下列条件中①∠1＝∠2； ②∠3＝∠4； ③∠2＋∠5＝∠6 ；④∠DAB＋∠2＋∠3＝180°，能判断AD∥BC的是（）

A . ①③④ B . ①②④ C . ①③ D . ①②③④

查看解析收藏纠错

+选题
3. 下列图形中，由∠1＝∠2，能得到AB∥CD的是（）.

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图，图中给出了过直线外一点作已知直线的平行线的方法，其依据的是（）

A . 同位角相等，两直线平行 B . 同旁内角互补，两直线平行 C . 内错角相等，两直线平行 D . 同平行于一条直线的两直线平行

查看解析收藏纠错

+选题
5.
如图，下列条件中能判定直线l₁∥l₂的是（）

A . ∠1=∠2 B . ∠1=∠5 C . ∠1+∠3=180° D . ∠3=∠5

查看解析收藏纠错

+选题
6. 如图，直线AC、DC、BE相交于点C，连接AB，能判定AB∥CD的条件是（）

A . ∠A=∠ACB B . ∠B=∠ACD C . ∠B+∠DCE=180° D . ∠A=∠ACD

查看解析收藏纠错

+选题
7. 给出下列说法：
（1）两条直线被第三条直线所截，同位角相等.（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交.（3）相等的两个角是对顶角.（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离.其中正确的有（）.

A . 0个 B . 1个 C . 2个 D . 3个

查看解析收藏纠错

+选题
8. 如图， $\text{[math]}$ ，则下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，给出下列条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 且 $\text{[math]}$ ；其中能推出 $\text{[math]}$ 的条件个数是（）

A . 0个 B . 1个 C . 2个 D . 3个

查看解析收藏纠错

+选题
10. 如图，由两个完全相同的三角板拼成一个四边形，则下列条件能直接判断 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. “过点P作直线b，使b∥a"，小明的作图痕迹如图所示，他的作法的依据是

查看解析收藏纠错

+选题
12. 如图，直线a，b被直线c所截，当∠1 ∠2时，a//b.（用“＞”，“＜”或“＝”填空）

查看解析收藏纠错

+选题
13. 将一副三角板如图摆放，则∥，理由是.

查看解析收藏纠错

+选题
14. 如图，不添加辅助线，请添加一个能判定 $\text{[math]}$ 的条件：．

查看解析收藏纠错

+选题
15. 如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3=∠4；（2）∠1=∠2；（3）∠A=∠DCE；（4）∠D+∠ABD=180°.能判断AB∥CD的有个.

查看解析收藏纠错

+选题
16. 如图，∠A＝70°，O是AB上一点，直线OD与AB的夹角∠BOD为75°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转度.

查看解析收藏纠错

+选题
17. 如图，要使AD//BF，则需要添加的条件是（写一个即可）.

查看解析收藏纠错

+选题
18. 如图，在三角形ABC中，点D ， E分别在边AC ， BC上，请你添加一个条件，使得DE $\text{[math]}$ AB ．（要求：不再添加辅助线，只需填一个答案即可）

查看解析收藏纠错

+选题

19. 小明在学习三角形的知识时，发现如下数学问题：
已知线段AB，CD交于点E，连结AD，BC．

（1）如图①，若∠D＝∠B＝100°，∠DAB的平分线与∠BCE的平分线交于点G，求∠G的度数；

（2）如图②，若∠D＝∠B＝90°，AM平分∠DAB，CF平分∠BCN，请判断CF与AM的位置关系，并说明理由．

查看解析收藏纠错

+选题
20. （问题情境）：如图 $\text{[math]}$ // $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
小明的思路是：过 $\text{[math]}$ 作 $\text{[math]}$ // $\text{[math]}$ ，通过平行线性质来求 $\text{[math]}$ .

（1）按小明的思路，求 $\text{[math]}$ 的度数；

（2）（问题迁移）：如图2，AB//CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

（3）（问题应用）：在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系.

查看解析收藏纠错

+选题
21. 下面是嘉琪同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程．

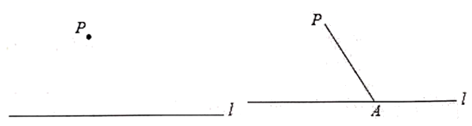
已知：如图，直线l和直线l外一点P ．

求作：直线PQ ，使直线PQ $\text{[math]}$ 直线l ．

作法：如图，

①在直线l上取一点A ，连接PA；

②作PA的垂直平分线MN ，分别交直线l ，线段PA于点B ， O；

③以O为圆心，OB长为半径作弧，交直线MN于另一点Q；

④作直线PQ ，所以直线PQ为所求作的直线．

根据上述作图过程，回答问题：

（1）用直尺和圆规，补全图中的图形（保留作图痕迹）；

（2）完成下面的证明：
证明：∵直线MN是PA的垂直平分线，

∴ ▲ ＝ ▲ ， ∠POQ＝∠AOB＝90°．

∴△POQ≌△AOB ．

∴ ▲ ＝ ▲ ，

∴PQ $\text{[math]}$ l（ ▲ ）（填推理的依据）．

查看解析收藏纠错

+选题
22. 如图，射线 $\text{[math]}$ 平外 $\text{[math]}$ ，且 $\text{[math]}$ .求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
23. 如图，AC//EF，∠1+∠3=180º．

（1） AF与CD是否平行？请说明理由；

（2）若AC平分∠FAB，AC⊥EB于点C，∠4=78º，求∠BCD的度数．

查看解析收藏纠错

+选题
24. 如图，已知点E在直线DC上，射线EF平分 $\text{[math]}$ ，过E点作 $\text{[math]}$ ，G为射线EC上一点，连接BG，且 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
25. 【学科融合】
物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）.由此可以归纳出如下的规律：

在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角.这就是光的反射定律（rfectionlaw）.

【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4.在这样的条件下，求证：AB∥CD.

【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD.

（1）如图2，光线AB与CD相交于点E，则∠BEC＝；

（2）如图3，光线AB与CD所在的直线相交于点E，CBED＝β，则α与β之间满足的等量关系是.

查看解析收藏纠错

+选题

2021-2022学年浙教版数学七下1.3平行线的判定同步练习

一、单选题

二、填空题

三、综合题

相关试卷收起∨

2021-2022学年浙教版数学七下1.3平行线的判定同步练习

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨