修改时间:2024-07-13 浏览次数:261 类型:中考真卷
|
已接种 |
未接种 |
合计 |
|
|
七年级 |
30 |
10 |
40 |
|
八年级 |
35 |
15 |
|
| 九年级 | 40 | | 60 |
| 合计 | 105 | | 150 |
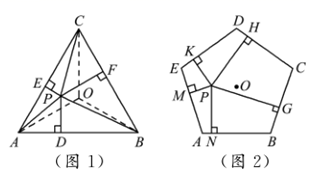
②如图2, 是边长为
的正五边形
内任意一点,设点
到五边形
各边距离分别为
,
,
,
,
,参照①的探索过程,试用含
的式子表示
的值.(参考数据:
,
)
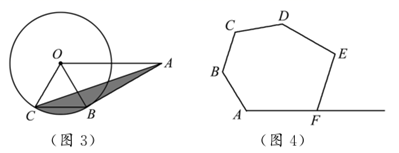
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造.若要将花坛形状改造成五边形
,其中点
在
的延长线上,且要保证改造前后花坛的面积不变,试确定点
的位置,并说明理由.
试题篮