修改时间:2021-07-01 浏览次数:548 类型:中考真卷
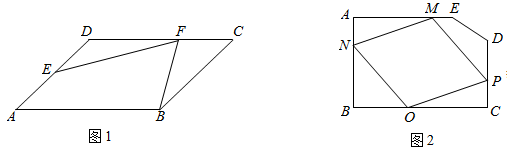
如图1,在 中,
,
,
,E是
的中点,点F在
上且
求四边形
的面积.(结果保留根号)
某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园 按设计要求,要在五边形河畔公园
内挖一个四边形人工湖
,使点O、P、M、N分别在边
、
、
、
上,且满足
,
.已知五边形
中,
,
,
,
,
.满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖
?若存在,求四边形
面积的最小值及这时点
到点
的距离;若不存在,请说明理由.
试题篮