初中数学苏科版九年级上册第三章综合测试卷

修改时间：2021-06-23 浏览次数：150 类型：单元试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A . 3个 B . 4个 C . 5个 D . 6个

查看解析收藏纠错

+选题
2. “实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值，是反映电动汽车性能的重要指标.某汽车厂家为了解某型号电动汽车的“实际平均续航里程”，收集了使用该型号电动汽车1年以上的部分客户相关数据，按年龄不超过40岁和年龄在40岁以上将客户分为A、B两组，从A、B组各抽取10位客户的电动汽车的“实际平均续航里程”数据整理成图，其中“⊙”表示A组的客户，“*”表示B组的客户.下列推断不正确的是（）

A . A组客户的电动汽车的“实际平均续航里程”的极差低于B组 B . A组客户的电动汽车的“实际平均续航里程”的方差低于B组 C . A组客户的电动汽车的“实际平均续航里程”的平均值低于B组 D . 这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组

查看解析收藏纠错

+选题
3. 一组数据2， $\text{[math]}$ ，4，3，3的平均数是3，则这组数据的中位数是（）

A . 2.5 B . 3 C . 3.5 D . 4

查看解析收藏纠错

+选题
4. 在一场排球比赛中，某排球队6名场上队员的身高（单位： $\text{[math]}$ ）是：180，184，188， 190，192，191，如果用一名身高为 $\text{[math]}$ 的队员替换场上身高为 $\text{[math]}$ 的队员，那么换人后与换人前相比，场上队员身高的平均数和方差大小变化正确的是（）

A . 平均数变小，方差变小 B . 平均数变小，方差变大 C . 平均数变大，方差变大 D . 平均数变大，方差变小

查看解析收藏纠错

+选题
5. 对于一组数据－1，2，－1， 4，下列结论不正确的是（）

A . 平均数是1 B . 众数是－1 C . 中位数是1.5 D . 方差是4.5

查看解析收藏纠错

+选题

6. 九年级（1）班甲、乙、丙、丁四名同学几次数学测试成绩的平均数 $\text{[math]}$ （分）及方差S²如下表：

	甲	乙	丙	丁
平均数（分）	95	97	95	97
方差	0.5	0.5	0.2	0.2

老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛，那么应选（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

7. 某校航模兴趣小组共有 30 位同学，他们的年龄分布如下表：

年龄/岁

13

14

15

16

人数

5

15

由于表格污损，15 岁和 16 岁的人数看不清，则下列关于年龄的统计量可以确定的是（）

A . 平均数、中位数 B . 众数、中位数 C . 平均数、方差 D . 中位数、方差

查看解析收藏纠错

+选题
8. 一组数据4，4，5，5，x，6，7的平均数是5，则这组数据的众数和中位数分别是（）

A . 4，5 B . 4，4 C . 5，4 D . 5，5

查看解析收藏纠错

+选题
9. 小红连续 $\text{[math]}$ 天的体温数据如下（单位相 $\text{[math]}$ ）： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .关于这组数据下列说法正确的是（）

A . 中位数是 $\text{[math]}$ B . 众数是 $\text{[math]}$ C . 平均数是 $\text{[math]}$ D . 极差是 $\text{[math]}$

查看解析收藏纠错

+选题
10. 某手表厂抽查了10只手表的日走时误差，数据如下表所示（单位： $\text{[math]}$ ）：

日走时误差

0

1

2

3

只数

3

4

2

1

则这10只手表的平均日走时误差（单位：s）是（）

A . 0 B . 0.6 C . 0.8 D . 1.1

查看解析收藏纠错

+选题

二、填空题

11. 一组数1、2、3、4、5的方差是 $\text{[math]}$ 与另一组数3、4、5、6、7的方差 $\text{[math]}$ 的大小比较 $\text{[math]}$ $\text{[math]}$ （填写：大于、等于、小于）.

查看解析收藏纠错

+选题
12. 某中学为了选拔一名运动员参加市运会 $\text{[math]}$ 米短比赛，有甲、乙两名运动员备选，他们最近测试的 $\text{[math]}$ 次百米跑平均时间都是 $\text{[math]}$ 秒，他们的方差分别是 $\text{[math]}$ （秒 $\text{[math]}$ ） $\text{[math]}$ （秒 $\text{[math]}$ ），如果要选择一名成绩优秀且稳定的人去参赛，应派去.

查看解析收藏纠错

+选题
13. 若一组数据1，3，5， $\text{[math]}$ ，的众数是3，则这组数据的方差为.

查看解析收藏纠错

+选题

14. 甲、乙两名射击运动员在平时某练习中的成绩如下表：

甲的成绩						乙的成绩
环数	7	8	9	10		环数	7	8	9	10
频数	2	3	3	2		频数	4	6	6	4

则甲、乙两名射击运动员在该练习中成绩的方差 $\text{[math]}$ 、 $\text{[math]}$ 的大小关系为.

查看解析收藏纠错

15. 一组数据4，4，5，5，x，6，7的平均数是5，则这组数据的中位数是.

查看解析收藏纠错

+选题
16. 在从小到大排列的五个数x，3，6，8，12中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为.

查看解析收藏纠错

+选题
17. 今年6月6日是第25个全国爱眼日，某校从八年级随机抽取50名学生进行了视力调查，并根据视力值绘制成统计图（如图），这50名学生视力的中位数所在范围是.

查看解析收藏纠错

+选题
18. 一组数据 $\text{[math]}$ 的平均数为.

查看解析收藏纠错

+选题
19. 一组数据：1，0，-1，x，2，若它们的平均数是1，则x=。

查看解析收藏纠错

+选题
20. 两组数据：3，a，2b，5与a，6，b的平均数都是6，若将这两组数据合并为一组数据，则这组新数据的众数为．

查看解析收藏纠错

+选题

三、解答题

21.
A，B，C三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表和图1：

（1）请将表和图1中的空缺部分补充完整．
（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图2（没有弃权票，每名学生只能推荐一个），则B在扇形统计图中所占的圆心角的度数是．
（3）若每票计1分，系里将笔试、口试、得票三项测试得分按4：3：3的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．

查看解析收藏纠错

+选题
22. 两组数据：3，m，2n，5与m，6，n的平均数都是6，若将这两组数据合并为一组数据，求这组新数据的中位数、众数、方差．

查看解析收藏纠错

+选题
23. 风景秀丽的红光村胜利水库承包给了养鱼专业户小李，他2001年投放了鲤鱼苗10000尾，成活率为70%，他2002年捕捞时，先随意捞出10鲤鱼，称得重量如下：（单位：千克）0.8 1.1 1.3 1.0 0.9 1.1 0.7 1.2 1.1 0.8
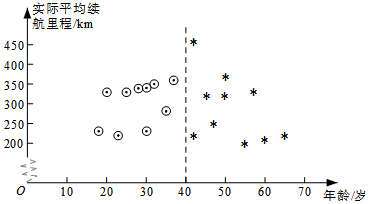
（1）回答下列问题：
①以上这组数据中，众数是多少，中位数是多少，样本平均数是多少；
②如果用样本平均数去估算小李放养的这批鲤鱼的总产量，并按每千克7元的价格全部卖掉，再扣除他这一年的投资成本（购鲤鱼苗、饲料等费用）1.9万元，上缴给红光村委会水库承包费1万元后，小李一年辛苦下来可得纯收入多少万元；
（2）小李设想在有了2002年的纯收入的基础上，今后按平均每年纯收入以相同的百分率增长、再经过两年的努力，到2004年的年纯收入能翻一番，然后将这三年纯收入的总和用于在水库旁建一个小型的农家乐，他请国土、建环等部门测算后知需要经费8.8万元，如果不考虑其它因素，请你为小李算一算，他的设想能实现吗？
（供参考数据： $\text{[math]}$ =1.414， $\text{[math]}$ =1.732）

查看解析收藏纠错

+选题
24.
射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如下：
甲：9，6，6，8，7，6，6，8，8，6；
乙：4，5，7，6，8，7，8，8，8，9．
如果你是教练员，会选择哪位运动员参加比赛？请说明理由．

查看解析收藏纠错

+选题
25. 康山村有村民300人，其中年收入800元的有150人，1500元的有100人，2000元的有45人，还有5人年收入100万元．根据这些数据计算该村人收入的平均数，中位数，众数．你认为这个数据中哪一个代表村民年收入的“平均水平”更合适？

查看解析收藏纠错

+选题
26. 在洋浦一新开业的以经营男式皮鞋为主的鞋店当服务员的阿丽是个做事善于观察的小姑娘，上班一段时间后，她发现各种尺码的男式皮鞋销量并不均衡，于是她把这个发现记录下来交给了她的老板：
尺码
37
38
39
40
41
42
43
销量（双）
12
15
22
28
32
30
4
你认为这个销售记录对老板管理鞋店生意有用吗？如果你认为有用，请说明你的理由，并请你帮这个老板策划一下如何利用这些信息？

查看解析收藏纠错

+选题
27. 某校初三学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是甲班和乙班成绩最好的5名学生的比赛成绩．

1号 2号 3号 4号 5号总数
甲班 100 98 102 97 103 500
乙班 99 100 95 109 97 500
经统计发现两班5名学生踢毽子的总个数相等．此时有学生建议，可以通过考查数据中的其它信息作为参考．
请你回答下列问题：
（1）甲乙两班的优秀率分别为、；
（2）计算两班比赛数据的方差；
（3）根据以上三条信息，你认为应该把团体第一名的奖状给哪一个班？简述理由．

查看解析收藏纠错

+选题
28.
射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示（折线图中，虚线表示甲，实线表示乙）：

（1）根据上图所提供的信息填写下表：

平均数众数方差
甲 7 ▲ ▲
乙 7 ▲ 2.2

（2）如果你是教练，会选择哪位运动员参加比赛？试说明理由．
（参考公式： $\text{[math]}$ ）

查看解析收藏纠错

+选题
29. 一次期中考试中，甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）

甲乙丙丁戊平均分标准差
数学 71 72 69 68 70
$\text{[math]}$
英语 88 82 94 85 76 85
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；（直接填入表格）
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，
标准分的计算公式：标准分＝(个人成绩－平均成绩)÷成绩标准差．
从标准分看，标准分大的考试成绩更好，请问甲同学在本次考试中，数学与英语哪个学科考得更好？

查看解析收藏纠错

+选题
30.
小明、小丽两位同学八年级10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如下图所示：

（1）根据上图中提供的数据填写下表：

平均成绩（分）中位数（分）众数（分）方差（S²）
小明 80
80
小丽
85
260
（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是谁？
（3）根据图表信息，请你对这两位同学各提一条不超过20个字的学习建议.

查看解析收藏纠错

+选题

四、综合题

31.

（1）【生活观察】甲、乙两人买菜，甲习惯买一定质量的菜，乙习惯买一定金额的菜，两人每次买菜的单价相同，例如：

菜价3元/千克

质量金额

甲 1千克 3元

乙 1千克 3元

菜价2元/千克

质量金额

甲 1千克    元

乙    千克 3元

①完成上表；

②计算甲两次买菜的均价和乙两次买菜的均价．（均价＝总金额÷总质量）

（2）【数学思考】设甲每次买质量为m千克的菜，乙每次买金额为n元的菜，两次的单价分别是a元/千克、b元/千克，用含有m、n、a、b的式子，分别表示出甲、乙两次买菜的均价 $\text{[math]}$ 、 $\text{[math]}$ .比较 $\text{[math]}$ 、 $\text{[math]}$ 的大小，并说明理由.

（3）【知识迁移】某船在相距为s的甲、乙两码头间往返航行一次，在没有水流时，船的速度为v所需时间为：如果水流速度为p时（p＜v），船顺水航行速度为（v+p），逆水航行速度为（v-p），所需时间为 $\text{[math]}$ 请借鉴上面的研究经验，比较 $\text{[math]}$ 、 $\text{[math]}$ 的大小，并说明理由.

查看解析收藏纠错

+选题
32. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图.请根据相关信息，解答下列问题：

（1）扇形统计图中，初赛成绩为1.65m所在扇形图形的圆心角为_°；

（2）补全条形统计图；

（3）这组初赛成绩的中位数是m；

（4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？

查看解析收藏纠错

+选题
33. 某公司共有A，B，C三个部门，根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表

部门

员工人数

每人所创的年利润/万元

A

5

10

B

b

8

C

5

（1） ①在扇形图中，C部门所对应的圆心角的度数为；
②在统计表中，b=，c=；

（2）求这个公司平均每人所创年利润.

查看解析收藏纠错

+选题

34. 某校组织学生参加“防疫卫生知识竞赛”（满分为100分）.竞赛结束后，随机抽取甲、乙两班各40名学生的成绩，并对数据（成绩）进行了整理、描述和分析.下面给出了部分信息.

信息一：甲、乙两班40名学生数学成绩的频数分布统计表如下：

成绩班级	50≤x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
甲	4	11	13	10	2
乙	6	3	15	12	2

（说明：成绩80分及以上为优秀，70～79分为良好，60～69分为合格，60分以下为不合格）

信息二：甲班成绩在70≤x＜80这一组的是：70，70，70，71，74，75，75，75，76，76，76，76，78

信息三：甲、乙两班成绩的平均分、中位数、众数如下：

班级	平均分	中位数	众数
甲	74.2	n	85
乙	73.5	73	84

根据以上信息，回答下列问题：

（1）写出表中n的值.

（2）在此次测试中，某学生的成绩是74分，在他所属班级排在前20名，由表中数据可知该学生是班的学生（填“甲”或“乙”），理由是.

（3）假设学校1200名学生都参加此次竞赛，估计成绩优秀的学生人数.

查看解析收藏纠错

35. 3月6日开学啦！为了解学生的体温情况，班主任张老师根据全班学生某天上午的《体温监测记载表》，绘制了如下不完整的频数分布表和扇形统计图.

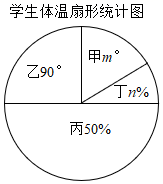
学生体温频数分布表

组别	温度（℃）	频数（人数）
甲	36.3	8
乙	36.4	a
丙	36.5	24
丁	36.6	4

请根据以上信息，解答下列问题：

（1）频数分布表中a＝，该班学生体温的众数是℃，中位数是℃；

（2）扇形统计图中甲所对应圆心角度数m°为＝度，丁组对应的扇形的圆心角是度；

（3）体温测量为36.6℃的4位同学中，男女生各两名，班主任准备从这四名同学中选出两名同学参加学校的新冠肺炎疫情防控知识宣传小组，请你用列表法或画树状图的方法求出所选两名同学正好都是女生的概率.

查看解析收藏纠错

36. 某工厂甲、乙两个部门各有员工400人，为了了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.

收集数据从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如表：

甲	78	86	74	81	75	76	87	70	75	90
甲	75	79	81	70	74	80	86	69	83	77
乙	93	73	88	81	72	81	94	83	77	83
乙	80	81	70	81	73	78	82	80	70	40

整理、描述数据按如下分数段整理、描述这两组样本数据：

成绩x人数

部门

40≤x≤49

50≤x≤59

60≤x≤69

70≤x≤79

80≤x≤89

90≤x≤100

甲

0

0

1

11

7

1

乙

1

0

0

7

10

2

（说明：成绩80分及以上为生产技能优秀，70～79分为生产技能良好，60～69分为生产技能合格，60分以下为生产技能不合格）

分析数据两组样本数据的平均数、中位数、众数如表所示：

部门	平均数	中位数	众数	方差
甲	78.3	77.5	m	33.61
乙	78	n	81	117.5

得出结论

（1）上表中m＝，n＝；

（2）甲、乙两个部门员工的生产技能水平比较均衡的是部门，估计乙部门生产技能优秀的员工人数为；

（3）可以推断出部门员工的生产技能水平较高，理由为.（至少从两个不同的角度说明推断的合理性）

查看解析收藏纠错

37. 某校为了解八年级学生课外阅读情况，随机抽取20名学生平均每周用于课外阅读的时间（单位：min），过程如表；

（收集数据）

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

（整理数据）

课外阅读时间x（min）	0≤x＜40	40≤x＜80	80≤x＜120	120≤x＜160
等级	D	C	B	A
人数	3	a	8	b

（分析数据）

平均数	中位数	众数
80	m	n

请根据以上提供的信息，解答下列问题：

（1）填空：a＝， b＝， m＝， n＝；

（2）如果每周用于课外阅读的时间不少于80min为达标，该校八年级现有学生800人，估计八年级达标的学生有多少人？

查看解析收藏纠错

38. 某中学九年级学生共进行了五次体育模拟测试，已知甲、乙两位同学五次模拟测试成绩的总分相同，小明根据甲同学的五次测试成绩绘制了尚不完整的统计表，并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表

次数

第一次

第二次

第三次

第四次

第五次

成绩（分）

35

39

37

$\text{[math]}$

40

小明将乙同学五次模拟测试成绩直接代入方差公式，计算过程如下：

$\text{[math]}$

根据上述信息，完成下列问题：

（1） a的值是；

（2）根据甲、乙两位同学这五次模拟测试成绩，你认为谁的体育成绩更好？并说明理由；

（3）如果甲再测试1次，第六次模拟测试成绩为38分，与前5次相比，甲6次模拟测试成绩的方差.（填“变大”“变小”或“不变”）

查看解析收藏纠错

+选题
39. 九年级某班女生进行为期一周的仰卧起坐训练，下面两图是该班女生训练前后“1分钟仰卧起坐”测试的成绩统计图.

（1）根据图1提供的信息，补全图2；

（2）下列说法正确的是（填写所有正确的序号）
①训练前该班女生的平均成绩是 $\text{[math]}$ 个；

②比较训练前后的成绩，共有3个成绩段的人数变化最大；

③训练前后成绩的中位数所在的成绩段由“36~38”变为“39~41”.

查看解析收藏纠错

+选题
40. 为了从小华和小亮两人中选拔一人参加射击比赛，现对他们的射击水平进行测试，两人在相同条件下各射击6次，命中的环数如下（单位：环）：
小华：7，8，7，8，9，9；小亮：5，8，7，8，10，10.

（1）填写下表：

平均数（环）

中位数（环）

方差（环²）

小华

8

小亮

8

3

（2）根据以上信息，你认为教练会选择谁参加比赛，理由是什么？

（3）若小亮再射击2次，分别命中7环和9环，则小亮这8次射击成绩的方差.（填“变大”、“变小”、“不变”）

查看解析收藏纠错

+选题

下载试卷答题卡下载在线测试收藏试卷分析试卷

相关试卷收起∨

试题篮