重庆市九龙坡区2021年数学中考适应性试卷

修改时间：2024-07-13 浏览次数：326 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. -2的绝对值是（）

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 在平面直角坐标系中，点 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列运算中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 气象局调查了甲、乙、丙、丁四个城市连续四年的降水量，它们的平均降水量都是323毫米，方差分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则这四个城市年降水量最稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

查看解析收藏纠错

+选题
5. 如图，线段 $\text{[math]}$ 两个端点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，以原点为位似中心，将线段 $\text{[math]}$ 放大得到线段 $\text{[math]}$ ，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四个人玩扑克牌游戏，他们先取出两张红桃和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色扑克牌的两个人为游戏搭档，若 $\text{[math]}$ 、 $\text{[math]}$ 两人各抽取了一张扑克牌，则两人恰好成为游戏搭档的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 某几何体三视图及相关数据如图所示，则该几何体的侧面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 在我国川西高原某山脉间有一河流，当河流中的水位上升到一定高度时因河堤承压有溃堤的危险．于是水利工程师在此河段的某处河堤上修了一个排水的预警水库联通另一支流．当河流的水位超过警戒位时就有河水流入预警的水库中，当水库有一定量的积水后，就会自动打开水库的排水系统流入另一支流．当河流的水位低于警戒位时水库的排水系统的排水速度则变慢．假设预警水库的积水时间为 $\text{[math]}$ 分钟，水库中积水量为 $\text{[math]}$ 吨，图中的折线表示某天 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系，下列说法中：
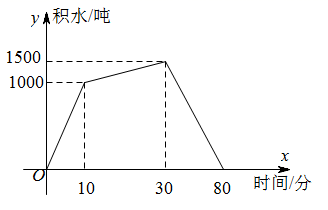
①这天预警水库排水时间持续了80分钟；②河流的水位超过警戒位时预警水库的排水速度比进水速度少25吨/分；③预警水库最高积水量为1500吨；④河流的水位低于警戒位时预警水库的排水速度为30吨/分．其中正确的信息判断是（）

A . ①④ B . ①③ C . ②③ D . ②④

查看解析收藏纠错

+选题
9. 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，直线 $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，点 $\text{[math]}$ 为半圆弧 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，已知等边 $\text{[math]}$ 的边长为1，作 $\text{[math]}$ 于点 $\text{[math]}$ ，在 $\text{[math]}$ 轴上取点 $\text{[math]}$ ，使 $\text{[math]}$ ，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ；作 $\text{[math]}$ 于点 $\text{[math]}$ ，在 $\text{[math]}$ 轴上取点 $\text{[math]}$ ，使 $\text{[math]}$ ，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ；作 $\text{[math]}$ 于点 $\text{[math]}$ ，在 $\text{[math]}$ 轴上取点 $\text{[math]}$ ，使 $\text{[math]}$ ，以 $\text{[math]}$ 为边作等边 $\text{[math]}$ ；…，且点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，…，都在第一象限，如此下去，则点 $\text{[math]}$ 的纵坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 若整数 $\text{[math]}$ 使得关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 且仅有3个整数解，且关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 的解为非负数，则所有满足条件的 $\text{[math]}$ 的值的个数为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
12. 如图，点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 、 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上， $\text{[math]}$ ， $\text{[math]}$ 过原点 $\text{[math]}$ ， $\text{[math]}$ 与反比例函数 $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上且 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 的面积为2，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 6 B . 9 C . 12 D . 18

查看解析收藏纠错

+选题

二、填空题

13. 使 $\text{[math]}$ 有意义的 $\text{[math]}$ 的取值范围是.

查看解析收藏纠错

+选题
14. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 某不透明容器的底面为正六边形（如图所示），将容器内掷一珠有弹性的橡皮球，则橡皮球恰好落在图中阴影部分的概率为．

查看解析收藏纠错

+选题
16. 已知 $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 为平行四边形， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为．

查看解析收藏纠错

+选题
17. 如图①是长方形纸带， $\text{[math]}$ ，将纸带沿 $\text{[math]}$ 折叠成图②，再沿 $\text{[math]}$ 折叠成图③，则图③中的 $\text{[math]}$ 的度数是度．

查看解析收藏纠错

+选题
18. 重庆市某服装厂配套生产一批校服，有领带、衬衫、丁恤三样.3月份，该厂家生产的领带、衬衫、丁恤的数量比是 $\text{[math]}$ ．进入4月份，春暖花开，气温上升，该厂家立刻又生产了一批这三样配套校服，其中衬衫增加的数量占总增加数量的 $\text{[math]}$ ，此时衬衫的总数量将达到三种服装总数量的 $\text{[math]}$ ，领带与T恤的数量比是 $\text{[math]}$ ．已知领带、衬衫、T恤这三样的成本价格分别是15元，60元，45元，厂家决定领带有 $\text{[math]}$ 作为促销礼物赠送，领带剩余部分按成本价格卖出，其余产品全部售出，最后三种服装的总利润率是50%，其中T恤的利润率为 $\text{[math]}$ ，则衬衫的售价是．元．（附：利润率=（售价-成本）÷成本×100%）

查看解析收藏纠错

+选题

三、解答题

19. 化简：

（1） $\text{[math]}$

（2） $\text{[math]}$

查看解析收藏纠错

+选题

20. 车厘子含铁量特别高，位于各种水果之首．一般情况下，车厘子果粒直径越大，级别越高，价格也越贵．现将车厘子果粒直径记为 $\text{[math]}$ （单位mm），车厘子一般分为5个等级，并给出相应的规格标示（以下简称：标示），具体是：一等 $\text{[math]}$ ，标示JJJJ；二等 $\text{[math]}$ ，标示JJJ；三等 $\text{[math]}$ ，标示JJ；四等 $\text{[math]}$ ，标示J；五等 $\text{[math]}$ ，标示XL．某商家准备选购一批车厘子，去智利、澳大利亚两个国家实地考察，在产地各随机抽取了20颗进行检测并统计这部分果粒的直径，相关数据整理如下：

（收集数据）

智利20颗车厘子果粒直径统计如下：

25，30.5，31，27，32.5，33.5，31，31.5，29，27.5，29，28.5，27，29，31.5，31，29，27.5，33.5，25.5

澳大利亚20颗车厘子果粒直径统计如下：

25，31，31，27，32.5，33.5，28.6，31，29，27.5，28，28.5，27，29，30，31，28.8，25.5，28.6，25.5

（整理数据）两组数据按等级分段，如下表所示：

国家	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
智利	2	4	5	$\text{[math]}$	3
澳大利亚	3	3	7	5	$\text{[math]}$

（分析数据）两组数据的平均数，中位数，众数如下表所示：

统计量	平均数	中位数	众数
智利	29.5	29	$\text{[math]}$
澳大利亚	28.9	$\text{[math]}$	31

（问题解决）根据以上信息，解答下列问题：

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

（2）若车厘子果粒直径 $\text{[math]}$ 为极品果，此时l公斤车厘子约有40颗，根据以上数据，商家最后决定在智利购买1000公斤车厘子，在澳大利亚购买200公斤车厘子，请估计商家购买到的极品果约为多少公斤？

（3）根据以上数据，如果只能在一个国家购买，你认为应该购买哪个国家的车厘子更好？请说明理由（写出一条理由即可）．

查看解析收藏纠错

+选题

21. 如图，已知四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 为平行四边形 $\text{[math]}$ 的对角线．

（1）请用直尺和圆规在 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ；

（2）在（1）的条件下，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
22. 在初中阶段的函数学习中，我们经历了列表、描点、连线、画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数 $\text{[math]}$ 的过程．

（1）已知函数过点 $\text{[math]}$ ，则这个函数的解析式为：．

（2）在（1）的条件下，在平面直角坐标系中，若函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴有两个交点，请画出该函数的图象，并写出函数图象的性质： ▲ （写出一条即可）．

（3）结合（2）中你所画的函数图象，求不等式 $\text{[math]}$ 的解集．

查看解析收藏纠错

+选题
23. 2020年上半年，我市出境旅游旅客的消费额比2019年同期相比至少下降了60%的消费．

（1）若2020年我市上半年出境旅游旅客消费额共计20亿元，则2019年我市出境旅游旅客消费额至少多少亿元？

（2）在疫情期间，我市 $\text{[math]}$ ， $\text{[math]}$ 两旅游公司的出境旅游业务也受到严重的影响．现知，我市 $\text{[math]}$ 旅游公司2019年出境旅游旅客消费额比2018年增长 $\text{[math]}$ ，但2020年比2019年出境旅游旅客消费额减少了 $\text{[math]}$ ； $\text{[math]}$ 旅游公司2020年出境旅游旅客消费额比 $\text{[math]}$ 旅游公司2019年出境旅游旅客消费额少 $\text{[math]}$ ．已知2020年 $\text{[math]}$ 、 $\text{[math]}$ 旅游公司出境旅游旅客消费总额是2018年 $\text{[math]}$ 旅游公司出境旅游旅客消费额的 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
24. 重庆市某校数学兴趣小组在水库某段 $\text{[math]}$ 的附近借助无人机进行实物测量的社会实践活动．如图所示，兴趣小组在水库正面左岸的 $\text{[math]}$ 处测得水库右岸 $\text{[math]}$ 处某标志物 $\text{[math]}$ 顶端的仰角为 $\text{[math]}$ ．在 $\text{[math]}$ 处一架无人飞机以北偏西 $\text{[math]}$ 方向飞行 $\text{[math]}$ 米到达点 $\text{[math]}$ 处，无人机沿水平线 $\text{[math]}$ 方向继续飞行30米至 $\text{[math]}$ 处，测得正前方水库右岸 $\text{[math]}$ 处的俯角为 $\text{[math]}$ ．线段 $\text{[math]}$ 的长为无人机距地面的铅直高度，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一条直线上．
（已知数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

（1）求无人机的飞行高度 $\text{[math]}$ ；

（2）求标志物 $\text{[math]}$ 的高度．（结果精确到0.1米）

查看解析收藏纠错

+选题
25. 如图，已知抛物线 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．-1，3是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个根．

（1）求该抛物线的解析式；

（2）过点 $\text{[math]}$ 作 $\text{[math]}$ 交抛物线于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ 为直线 $\text{[math]}$ 上方抛物线上的一个动点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值及此时点 $\text{[math]}$ 的坐标；

（3）在（2）的条件下，点 $\text{[math]}$ 为抛物线上一动点，在平面内找一点 $\text{[math]}$ ，是否存在以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是以 $\text{[math]}$ 为边的矩形？若存在，请直接写出点 $\text{[math]}$ 的坐标，若不存在，请说明理由．

查看解析收藏纠错

+选题
26. 如图l，四边形 $\text{[math]}$ 为菱形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上任意一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上任意一点．

（1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长（用 $\text{[math]}$ 表示）．

（2）如图2，作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 存在的数量关系，并证明你猜想的结论．

（3）在点 $\text{[math]}$ 的运动过程中，当 $\text{[math]}$ 的值最小时，请直接写出 $\text{[math]}$ 的长（用 $\text{[math]}$ 表示）．

查看解析收藏纠错

+选题

重庆市九龙坡区2021年数学中考适应性试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨