陕西省学林2021年数学中考模拟大联考试卷（一）

修改时间：2021-06-19 浏览次数：484 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 计算（﹣ $\text{[math]}$ ）⁰＝（）

A . ﹣ $\text{[math]}$ B . 1 C . ﹣4 D . ﹣1

查看解析收藏纠错

+选题
2. 两个长方体按图示方式摆放，其主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 如图，直线a，b相交于点O，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 如表中是正比例函数y＝kx的自变量x与函数y的对应值，则P的值为（）

x

﹣2

1

y

4

p

A . 2 B . ﹣2 C . 1 D . 4

查看解析收藏纠错

+选题
5. 下列计算正确的是（）

A . 3a+2b＝5ab B . a³•a²＝a⁶ C . （﹣a³b）²＝a⁶b² D . a²b³÷a＝b³

查看解析收藏纠错

+选题
6. 如图， $\text{[math]}$ 中，AB＝AC，AD⊥BC于点D，DE⊥AB于点E，BF⊥AC于点F，DE＝2，则BF的长为（）

A . 4 B . 3 C . 5 D . 6

查看解析收藏纠错

+选题
7. 把直线 $\text{[math]}$ 向右平移2个单位可以得到直线 $\text{[math]}$ ，要得到直线 $\text{[math]}$ ，也可以把直线 $\text{[math]}$ （）

A . 向上平移2个单位 B . 向下平移2个单位 C . 向上平移6个单位 D . 向下平移6个单位

查看解析收藏纠错

+选题
8. 如图，菱形 $\text{[math]}$ 对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .若菱形 $\text{[math]}$ 的面积为4，则菱形的边长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
9. 如图，点A，D，B，C是圆O上的四个点，连接AB，CD，相交于点E，若∠BOD＝40°，∠AOC＝120°，则∠AEC等于（）

A . 70° B . 75° C . 80° D . 85°

查看解析收藏纠错

+选题
10. 已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值不可能是（）

A . -2 B . $\text{[math]}$ C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

11. 比较大小：﹣3 $\text{[math]}$ ﹣4.（填“＞”“＜”或“＝”）

查看解析收藏纠错

+选题
12. 如图，正六边形 $\text{[math]}$ 的边长为2，则 $\text{[math]}$ 的周长为.

查看解析收藏纠错

+选题
13. 在平面直角坐标系中，A为反比例函数y＝﹣ $\text{[math]}$ （x＞0）图象上一点，点B的坐标为(4，0)，O为坐标原点，若 $\text{[math]}$ 的面积为6，则点A的坐标为.

查看解析收藏纠错

+选题
14. 如图，在矩形ABCD中，AB＝4，AD＝6，点E是AD所在直线上的一点，过点A作AN⊥BE于N，点M是BC上一动点，连接NM，MD，则MN+MD的最小值为.

查看解析收藏纠错

+选题

三、解答题

15. 解不等式组： $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 化简：（ $\text{[math]}$ ﹣a+1）÷ $\text{[math]}$ .

查看解析收藏纠错

+选题
17. 如图，在 $\text{[math]}$ 中，∠A＝30°，请用尺规作图法，在AC边上求作一点M，使得AM＝2BM.（不写作法，保留作图痕迹）

查看解析收藏纠错

+选题
18. 如图，在▱ABCD中，点E，F是对角线AC上的两点，且AF=CE，连接DE，BF.求证：DE∥BF.

查看解析收藏纠错

+选题

19. 为保护学生视力，让学生在学校专心学习，防止沉迷网络和游戏，促进学生身心健康发展，2021年2月1日教育部印发《关于加强中小学生手机管理工作的通知》，要求中小学生原则上不得将个人手机代入校园.某校为了解全校学生在此之前使用手机情况，随机抽取了部分学生调查其一周使用手机的时间，并用调查结果绘制了如下统计图表，请根据统计图表解答以下问题：

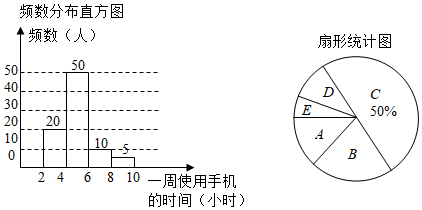
组别	使用时间t（小时）
A	0＜t≤2
B	2＜t≤4
C	4＜t≤6
D	6＜t≤8
E	8＜t≤10

（1）补全频数分布直方图，填出所抽取学生一周使用手机时间的中位数落在组；

（2）若以各组组中值（例如0＜t≤2的组中值为1小时）代表各组的实际数据，求出所抽取学生一周使用手机时间的平均数及众数；

（3）若该校共有1200名中学生，请你估计该校学生中一周使用手机的时间在6小时以上的有多少人？

查看解析收藏纠错

+选题

20. 2020年我国建成5G基站超60万个，5G建设跑出“中国速度”.某地有一个5G信号塔AB，小敏想用所学的数学知识测量信号塔AB的高度，她选择用树CD和楼房来测量.首先在树的底部D处测得信号塔的顶部A的仰角为42°；然后她站在楼房上的点E处恰好看到树的顶端C、信号塔的顶端A在一条直线上.测得树与楼房的距离DF＝12米，CD＝12米，EF＝6米，已知点B、D、F三点共线，AB⊥BF，CD⊥BF，EF⊥BF，测量示意图如图所示.请根据相关测量信息，求信号塔AB的高度.（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

查看解析收藏纠错

+选题
21. 为全面落实乡村振兴总要求，充分发扬“为民服务孺子牛”“创新发展拓荒牛”“艰苦奋斗老黄牛”精神，某镇政府计划在该镇试种植苹果树和桔子树共100棵.已知平均每棵果树的投入成本和产量如表所示，且苹果的售价为10元/kg，桔子的售价为6元/kg.

成本（元/棵）

产量（kg/棵）

苹果树

120

30

桔子树

80

25

设种植苹果树x棵.

（1）若种植苹果树和桔子树共获利y元，求y与x之间的函数关系式；

（2）若种植苹果树45棵，求种植苹果树和桔子树共获利多少元？

查看解析收藏纠错

+选题
22. 嫦娥、神舟、北斗、天问被称为中国航天的“四大天王”.2020年“北斗”组网、“天问”问天、“嫦五”探月，一个个好消息从太空传来，照亮了中国航天界的未来!小玲对航空航天非常感兴趣，她收集到了嫦娥五号、神舟十一号、北斗三号、天问一号的模型图，依次制成编号为A、B、C、D的四张卡片（背面完全相同），将这四张卡片背面朝上，洗匀放好.

（1）小玲从中随机抽取一张卡片是“北斗三号”的概率为；

（2）小玲从四张卡片中随机抽取一张卡片（不放回）.再从余下的卡片中随机抽取一张，请用列表或画树状图的方法求抽到的两张卡片恰好是编号为A（嫦娘五号）和D（天问一号）的概率.

查看解析收藏纠错

+选题
23. 如图，作 $\text{[math]}$ 的外接圆⊙O，AB为⊙O的直径，点D在AB上（D不与端点重合），过点D作AB的垂线交BF的延长线于点C，且CD＝AB，过F作⊙O的切线交DC于点E.

（1）求证：EF＝EC；

（2）若D是OA的中点，AB＝4，求CF的长.

查看解析收藏纠错

+选题
24. 如图，已知抛物线L：y＝x²+bx﹣4交y轴于点A，交x轴于点B(﹣4，0)、C.抛物线L关于原点O对称的抛物线为 $\text{[math]}$ ，点A在抛物线 $\text{[math]}$ 上的对应点为A'.

（1）求抛物线 $\text{[math]}$ 的函数表达式；

（2）过点 $\text{[math]}$ 作平行于x轴的直线l，点P是抛物线 $\text{[math]}$ 上一动点，过点P作PQ⊥l于Q，连接 $\text{[math]}$ .若 $\text{[math]}$ ，求点P的坐标.

查看解析收藏纠错

+选题
25. 问题提出

（1）如图1， $\text{[math]}$ 中，∠B＝90°，∠A＝30°，BC＝a，则 $\text{[math]}$ 的面积为；（用含a的式子表示）

（2）如图2， $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，点B，D，E在同一条直线上，求∠BEC的度数；

（3）问题解决
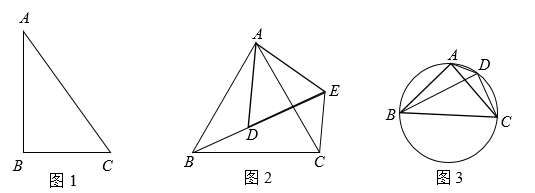
为迎接2021年陕西全运会，某地在街心花园中规划出一块如图3所示的圆形土地，用于种植花卉和草坪.已知 $\text{[math]}$ 与 $\text{[math]}$ 均为圆的内接三角形， $\text{[math]}$ ＝ $\text{[math]}$ ，点D在 $\text{[math]}$ 上，∠BDC＝2∠ADB，BD＝120m.现准备在△ABC区域内种植红色花卉，在 $\text{[math]}$ 区域内种植白色花卉，圆内其余区域为草坪.种植这种红色花卉每平方米需20元.设AD的长为x（m），种植红色花卉的费用是y（元）.

①求y与x之间的函数关系式；

②若种植这种白色花卉每平方米需60元，求种植这种红色花卉和白色花卉所需的总费用最多是多少？

查看解析收藏纠错

+选题

	成本（元/棵）	产量（kg/棵）
苹果树	120	30
桔子树	80	25

x	﹣2	1
y	4	p

陕西省学林2021年数学中考模拟大联考试卷（一）

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨