湘教版备考2021年中考数学二轮复习专题18数据的收集与分析

1. 若一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数为4，方差为3，那么数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平均数和方差分别是（）

A . 4， 3 B . 6 $\text{[math]}$ 3 C . 3 $\text{[math]}$ 4 D . 6 5

查看解析收藏纠错

+选题
2. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A . 平均数和中位数不变 B . 平均数增加，中位数不变 C . 平均数不变，中位数增加 D . 平均数和中位数都增大

查看解析收藏纠错

+选题
3. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 为了了解2019年石家庄市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩。下列说法正确的是（）

A . 2019年石家庄市九年级学生是总体 B . 每一名九年级学生是个体 C . 1000名九年级学生是总体的一个样本 D . 样本容量是1000

查看解析收藏纠错

+选题
5. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A . 平均数为10，方差为2 B . 平均数为11，方差为3 C . 平均数为11，方差为2 D . 平均数为12，方差为4

查看解析收藏纠错

+选题
6. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A . 3个 B . 4个 C . 5个 D . 6个

查看解析收藏纠错

+选题
7. 小华进行了5次射击训练后，计算出这5次射击的平均成绩为8环，方差为s₁² ，随后小华又进行了第6次射击，成绩恰好是8环，并计算出这6次射击成绩的方差为s₂² ，则下列说法正确的是（）

A . s₁²=s₂² B . s₁²＜s₂² C . s₁²＞s₂² D . 无法确定s₁²与s₂²的大小

查看解析收藏纠错

+选题
8. 某次校运会共有13名同学报名参加百米赛跑，他们的预赛成绩各不相同，现取其中前6名参加决赛，小勇同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这13名同学成绩的（）

A . 平均数 B . 众数 C . 中位数 D . 方差

查看解析收藏纠错

+选题
9. 一组数据2， $\text{[math]}$ ，4，3，3的平均数是3，则这组数据的中位数是（）

A . 2.5 B . 3 C . 3.5 D . 4

查看解析收藏纠错

+选题

10. 某一段时间，小芳测得连续五天的日最低气温后，整理得出表（有两个数据被遮盖），被遮盖的两个数据依次是（）

日期	一	二	三	四	五	方差	平均气温
最低气温	1℃	﹣1℃	2℃	0℃	■	■	1℃

A . 3℃，2 B . 3℃， $\text{[math]}$ C . 2℃，2 D . 2℃， $\text{[math]}$

查看解析收藏纠错

+选题

11. 已知一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数为.

查看解析收藏纠错

+选题
12. 某学校九（1）班40名同学的期中测试成绩分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，……， $\text{[math]}$ .已知 $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +……+ $\text{[math]}$ = 4800，y= $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +……+ $\text{[math]}$ ，当y取最小值时，的值为.

查看解析收藏纠错

+选题
13. 已知数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的方差是 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的方差为.

查看解析收藏纠错

+选题
14. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看解析收藏纠错

+选题
15. 在抗击新型冠状病毒疫情期间，某校学生主动发起为武汉加油捐款活动，为了了解学生捐款金额（单位：元），随机调查了该校的部分学生，根据调查结果，绘制出如图的统计图.统计的这组学生捐款数据的众数是，中位数是.

查看解析收藏纠错

+选题

16. 某农科所甲、乙试验田各有水稻3万个，为了考察水稻穗长的情况，于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量，获得了它们的长度x（单位：cm），并对数据（穗长）进行了整理、描述和分析．下面给出了部分信息．

a ．甲试验田穗长的频数分布统计表如表1所示（不完整）：

甲试验田穗长频数分布表（表1）

分组/cm	频数	频率
4.5≤x $\text{[math]}$ 5	4	0.08
5≤x $\text{[math]}$ 5.5	9	0.18
5.5≤x $\text{[math]}$ 6		n
6≤x $\text{[math]}$ 65	11	0.22
6.5≤x $\text{[math]}$ 7	m	0.20
7≤x $\text{[math]}$ 7.5	2
合计	50	1.00

b ．乙试验田穗长的频数分布直方图如图1所示：

c ．乙试验田穗长在6≤x $\text{[math]}$ 6.5这一组的是：6.3，6.4，6.3，6.3，6.2，6.2，6.1，6.2，6.4

d ．甲、乙试验田穗长的平均数、中位数、众数、方差如下（表2）：

试验田	平均数	中位数	众数	方差
甲	5.924	5.8	5.8	0.454
乙	5.924	w	6.5	0.608

根据以上信息，回答下列问题：

（1）表1中m的值为，n的值为；

（2）表2中w的值为；

（3）在此次考察中，穗长为5.9cm的稻穗，穗长排名（从长到短排序）更靠前的试验田是；稻穗生长（长度）较稳定的试验田是；

A ．甲 B ．乙 C ．无法推断

（4）若穗长在5.5≤x $\text{[math]}$ 7范围内的稻穗为“良好”，请估计甲试验田所有“良好”的水稻约为万个．

查看解析收藏纠错

+选题

17. 某少年军校准备从甲，乙，丙三位同学中选拔一人参加全市射击比赛，他们在选拔比赛中，射靶十次的平均环数是 $\text{[math]}$ = $\text{[math]}$ ＝ $\text{[math]}$ =8.3，方差分别是 $\text{[math]}$ =1.5， $\text{[math]}$ =2.8， $\text{[math]}$ =3.2.那么，根据以上提供的信息，你认为应该推荐参加全市射击比赛的同学是 .

查看解析收藏纠错

+选题

18. 入为响应习近平提出的“绿水青山就是金山银山”的重要思想某校举办了“绿水青山，生态文明”知识竞赛(竞每一项的满分10分，学生得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀，他们的四项成绩分布的条形统计图如图所示根据上图结果解答下列问题。

（1）补充完成下表
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分²)
张山
9

9

李仕

9.5

1.5

（2）根据(1)题数据，分别从中位数、方差两个角度比较说明两位同学的各自优势?

（3）若实践操作、环保论文、现场抢答、笔试得分技4：1：2：3的比例折合成综合得分，请通过计算说明哪位同学的综合得分更高。

查看解析收藏纠错

+选题
19. 某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了如图①②两幅不完整的统计图，请根据图中的信息解答下列问题．

（1）九年级(1)班接受调查的学生共有多少名？

（2）补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数．

查看解析收藏纠错

+选题

20. “节约用水、人人有责”，某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计，发现5月份各户居民的用水量比4月份有所下降，并且将5月份各户居民的节水量统计整理成如图所示的统计图表
节水量/立方米
1
1.5
2.5
3
户数/户
50
80
a
70

（1）写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数．

（2）根据题意，将5月份各居民的节水量的条形统计图补充完整．

（3）求该小区300户居民5月份平均每户节约用水量，若用每立方米水需4元水费，请你估算每户居民1年可节约多少元钱的水费？

查看解析收藏纠错

+选题
21. 为了解某县2014年初中毕业生的实验成绩等级的分布情况，随机抽取了该县若干名学生的实验成绩进行统计分析，并根据抽取的成绩绘制了如图所示的统计图表：
成绩等级
A
B
C
D
人数
60
x
y
10
百分比
30%
50%
15%
m

请根据以上统计图表提供的信息，解答下列问题：

（1）本次抽查的学生有名；

（2）表中x，y和m所表示的数分别为：x=，y=，m=；

（3）请补全条形统计图；

（4）若将抽取的若干名学生的实验成绩绘制成扇形统计图，则实验成绩为D类的扇形所对应的圆心角的度数是多少．

查看解析收藏纠错

+选题
22. 某校九年级（1）班的一个数学学习小组对全班某次测试中的“一道满分值为6分的解答题得分”情况进行了统计，绘制成下列不完整的统计图（学生得分均为整数）：

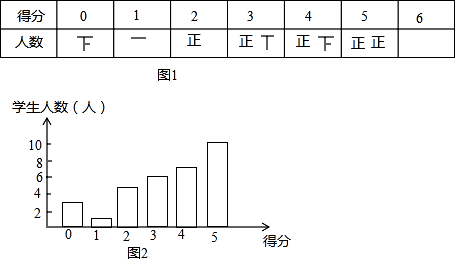
已知全班同学此题的平均得分为4分，结合表格解决下列问题：

（1）完成表格，并求该班学生总数；

（2）根据表中提供的数据，补全条形统计图；并判断下列说法中正确的有．（填序号即可）
①该班此题得分的众数是6；

②“随机抽取该班一份试卷，此题得1分”是不可能事件；

③该班学生此题得分的中位数是4；

④若将“该班同学本道题的得分情况”绘制成扇形统计图，求“此题得0分”的人数所对应的圆心角的度数为36°；

（3）若本年级学生共有540人，请你估计整个年级中此题得满分的学生人数．

查看解析收藏纠错

+选题

23. 某校八年级(3)班40个学生某次数学测验成绩如下：
63，84，91，53，69，81，61，69，91，78，
75，81，80，67，76，81，79，94，61，69，
89，70，70，87，81，86，90，88，85，67，
71，82，87，75，87，95，53，65，74，77.
数学老师按10分的组距分段，算出每个分数段学生成绩出现的频数，填入频数分布表(表1)：
表1
成绩段
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~99.5
划记
T
正正
正正
正正正
正
频数
2
9
______
14
5
频率
0.050
0.225
0.250
0.350
______

（1）请把频数分布表(表1)、频数分布直方图(图1)补充完整.

（2）请你帮老师统计一下这次数学考试的及格率(不低于60分为及格)及优秀率(不低于90分为优秀).

（3）哪个分数段的学生最多?哪个分数段的学生最少?

查看解析收藏纠错

+选题
24. 随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天；B．学习；C．购物；D．游戏；E．其它），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到图表（部分信息未给出）：

根据以上信息解答下列问题：

（1）这次被调查的学生有多少人？

（2）求表中m，n，p的值，并补全条形统计图．

（3）若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议．

查看解析收藏纠错

+选题

25. 9月16日，2020线上智博会举行西部（重庆）科学城新闻发布会.会上透露，西部（重庆）科学城是“科学家的家、创业者的城”，力争到2035年，全面建成具有全国影响力的科技创新中心核心区.为了解民众对科学城相关知识的知晓程度，某公司派甲、乙两人各随机调查20名群众，填写了对科学城相关知识的调查问卷（满分为10分），得分用x表示（x为整数），数据分组为 A：0≤x＜2，B：2≤x＜4，C：4≤x＜6，D：6≤x＜8，E：8≤x≤10）.对问卷得分进行整理分析，给出了下面部分信息：

甲问卷得分的扇形统计图

乙问卷得分频数分布直方图（人数）

两组问卷得分的平均数，中位数，众数，满分率如下表：

	平均数（分）	中位数（分）	众数（分）	满分率
甲公司	5.15	n	6	5%
乙公司	5.55	6	P	5%

甲公司B组占10%，E组占30%，A圆心角度数 $\text{[math]}$ ；

甲公司分数在C、D组的数据为：6，4，4，6，6，7，6，5；乙公司E组所有数据之和为58.

根据以上信息，解答下列问题：

（1）扇形统计图中 $\text{[math]}$ ＝度，信息表中的中位数n＝分，众数P＝分；

（2）通过以上数据分析，你认为公司问卷调查的成绩更好，理由是；（写一条即可）

（3）若分数大于等于6即为合格，请估计问卷调查1600名群众中合格的人数是多少？

查看解析收藏纠错

+选题

26. 由于疫情的影响，学生不能返校上课，某校在直播授课的同时还为学生提供了四种辅助学习方式：A网上自测，B网上阅读，C网上答疑，D网上讨论。为了解学生对四种学习方式的喜欢情况，该校随机抽取部分学生进行问卷调查，规定被调查学生从四种方式中选择自己最喜欢的一种，根据调查结果绘制成如图两幅不完整的统计图：
根据统计图提供的信息，解答下列问题：

（1）本次共调查了名学生；并请补全条形统计图；

（2）在扇形统计图中，m的值是，D对应的扇形圆心角的度数是；

（3）若该校共有2000名学生，根据抽样调查的结果，请你估计该校最喜欢方式D的学生人数。

查看解析收藏纠错

+选题
27. 某校为了在七年级600名学生中顺利开展“四点半”课堂，采用随机抽样的方法，从喜欢乒乓球、跳绳、篮球、绘画四个方面调查了若干名学生，并绘制了条形统计图和扇形统计图，请结合两幅统计图，回答下列问题：

（1）这次调查活动中，一共调查了名学生；

（2） “乒乓球”所在扇形的圆心角是度；

（3）请补全条形统计图；

（4）根据本次调查情况，请你估计七年级600名学生中喜欢“乒乓球”的人数有多少？

查看解析收藏纠错

+选题
28. 甲、乙两支运动队各有10名队员，他们的年龄分布情况分别如图、表所示：

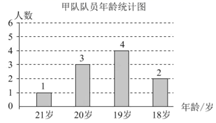
甲、乙两队队员年龄统计表

平均数（近似值）

众数

中位数

甲队

a

①

②

乙队

20

③

b

解决下列问题：

（1）求甲队队员的平均年龄a的值．（结果取整数）

（2）补全统计表中的①②③三处．

（3）阅读理解-----扇形图中求中位数的方法．
[阅读与思考]

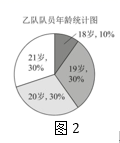
小明同学在求乙队队员年龄的中位数b时，是这样思考的：因为中位数是将一组数据按大小排序后，排在中间位置的一个数或中间两个数的平均数，那就需要先找到数据按大小排序后，大致排在50%附近的数，再根据中位数的概念进行细化求解．

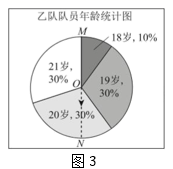
图2这个扇形图中的数据18~21是按大小顺序旋转排列的，我们就可以像图3所示的这样，先找到最大数据“21”与最小数据“18”的分界半径OM，为找到排在50%附近的数，再作出直径MN，那么射线ON指向的数据就是中位数．

王老师的评价：小明的这个方法是从中位数的概念出发，充分利用了扇形图的特性形象直观地解决问题．

[理解与应用]

请你利用小明的方法直接写出统计表中b的值．

查看解析收藏纠错

+选题
29. 某校九年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：

（1）样本容量是，并补全直方图；

（2）该年级共有学生800人，请估计该年级在这天里发言次数不少于12次的人数；

（3）已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好都是男生的概率.

查看解析收藏纠错

+选题
30. 某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：

（1）请将下表补充完整：（参考公式：方差 $\text{[math]}$ ）

平均数

方差

中位数

甲

7

①.

7

乙

②.

5.4

③.

（2）请从下列三个不同的角度对这次测试结果进行分析：①从平均数和方差相结合看，的成绩好些；②从平均数和中位数相结合看，的成绩好些；

（3）若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．

查看解析收藏纠错

+选题

31. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：

根据以上信息，整理分析数据如下：

	平均成绩/环	中位数/环	众数/环	方差
甲	a	7	7	1.2
乙	7	b	8	c

（1）写出表格中a，b，c的值：a＝，b＝，c＝.

（2）如果乙再射击一次，命中7环，那么乙的射击成绩的方差.（填“变大”“变小”“不变”）

（3）教练根据这10次成绩若选择甲参加比赛，教练的理由是什么？

查看解析收藏纠错

+选题

湘教版备考2021年中考数学二轮复习专题18数据的收集与分析

一、单选题

二、填空题

三、计算题

四、解答题

五、作图题

六、综合题

相关试卷收起∨

姓名	平均成绩(分)	中位数(分)	众数(分)	方差(分²)
张山	9		9
李仕		9.5		1.5

成绩段	49.5~59.5	59.5~69.5	69.5~79.5	79.5~89.5	89.5~99.5
划记	T	正正	正正	正正正	正
频数	2	9	______	14	5
频率	0.050	0.225	0.250	0.350	______

	平均数（近似值）	众数	中位数
甲队	a	①	②
乙队	20	③	b

数据	37	38	39	40	41
频数	8	4	5	a	1

节水量/立方米	1	1.5	2.5	3
户数/户	50	80	a	70

成绩等级	A	B	C	D
人数	60	x	y	10
百分比	30%	50%	15%	m

湘教版备考2021年中考数学二轮复习专题18数据的收集与分析

一、单选题

二、填空题

三、计算题

四、解答题

五、作图题

六、综合题

相关试卷 收起∨

相关试卷收起∨