修改时间:2024-07-13 浏览次数:210 类型:期末考试
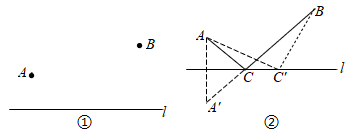
为了证明点C的位置即为所求,不妨在直线l上另外任取一点C',连接AC'、BC',证明AC+CB<AC'+C'B.请完成这个证明.

老师在课堂上给出了这样一道题目:如图,在△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.试探究线段BE和CD的数量关系.小明同学经过认真思考后认为:先延长CA、BE相交于点为F,再证明△ACD≌△ABF即可,请根据小明同学的思路补全图形并直接写出线段BE和CD的数量关系.
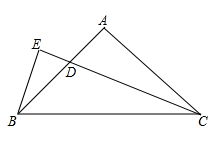
老师引导同学们继续研究:
如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB= ∠C,BE⊥DE,垂足为E,DE与AB相交于点F,试探究线段BE与FD的数量关系,并证明你的结论.

试题篮