北京市通州区2020年中考数学一模试卷

修改时间：2024-11-06 浏览次数：217 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 在疫情防控的特殊时期，为了满足初三高三学生的复习备考需求，北京市教委联合北京卫视共同推出电视课堂节目《老师请回答特别节目“空中课堂”》，在节目播出期间．全市约有200000名师生收看了节目．将200000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列图形中，是轴对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
3. 在数轴上，表示实数a的点如图所示，则2-a的值可以为（）

A . -5.4 B . -1.4 C . 0 D . 1.4

查看解析收藏纠错

+选题
4. 以 $\text{[math]}$ 为边画出四边形 $\text{[math]}$ ，可以画出的四边形个数为（）

A . 0 B . 1 C . 2 D . 无限多

查看解析收藏纠错

+选题
5. 在一个长 $\text{[math]}$ 分米、宽 $\text{[math]}$ 分米、高 $\text{[math]}$ 分米的长方体容器中，水面高 $\text{[math]}$ 分米，把一个实心铁块缓慢浸入这个容器的水中，能够表示铁块浸入水中的体积y(单位：立方分米)与水面上升高度x(单位：分米)之间关系的图象的是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 如果 $\text{[math]}$ 那么代数式 $\text{[math]}$ 的值是（）

A . 3 B . 1 C . -1 D . -3

查看解析收藏纠错

+选题
7. 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 的图象如图所示，则a的值可以为（）

A . 0.7 B . 0.9 C . 2 D . 2.1

查看解析收藏纠错

+选题

8. 改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月 $\text{[math]}$ 两种移动支付方式的使用情况，从全校1000名学生中随机抽取了100人，发现样本中 $\text{[math]}$ 两种支付方式都不使用的有5人，样本中仅使用 $\text{[math]}$ 种支付方式和仅使用 $\text{[math]}$ 种支付方式的学生的支付金额a(元)的分布情况如下：

支付金额 $\text{[math]}$ （元）

支付方式

$\text{[math]}$

仅使用 $\text{[math]}$

18人

9人

3人

仅使用 $\text{[math]}$

10人

14人

1人

下面有四个推断：

①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率大于他使用B支付方式的概率；②根据样本数据估计，全校1000名学生中．同时使用A、B两种支付方式的大约有400人；③样本中仅使用A种支付方式的同学，上个月的支付金额的中位数一定不超过1000元；④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数一定不低于1000元．其中合理的是（）

A . ①③ B . ②④ C . ①②③ D . ①②③④

查看解析收藏纠错

+选题

二、填空题

9. 举出一个数字“0”表示正负之间分界点的实际例子，如．

查看解析收藏纠错

+选题
10. 若某个正多边形的一个内角为 $\text{[math]}$ ，则这个正多边形的内角和为.

查看解析收藏纠错

+选题
11. 若 $\text{[math]}$ ，则 $\text{[math]}$ 可以用含 m、n 的代数式表示为．

查看解析收藏纠错

+选题
12. 把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形，将这四个全等的直角三角形拼成图2所示的正方形，则图2中小正方形ABCD的面积为．

查看解析收藏纠错

+选题

13. 某班甲、乙、丙三名同学20天的体温数据记录如下表：

甲的体温					乙的体温					丙的体温
温度（℃）	36.1	36.4	36.5	36.8	温度（℃）	36.1	36.4	36.5	36.8	温度（℃）	36.1	36.4	36.5	36.8
频数	5	5	5	5	频数	6	4	4	6	频数	4	6	6	4

则在这20天中，甲、乙、丙三名同学的体温情况最稳定的是．

查看解析收藏纠错

+选题

14. 如图将一张矩形纸片ABCD沿对角线BD翻折，点C的对应点为C′，AD与BC′交于点E ，若∠ABE＝30°，BC＝3，则DE的长度为．

查看解析收藏纠错

+选题
15. 一笔总额为1078元的奖金，分为一等奖、二等奖和三等奖，奖金金额均为整数，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍，若把这笔奖金发给6个人，评一、二、三等奖的人数分别为 $\text{[math]}$ ，且 $\text{[math]}$ ，那么三等奖的奖金金额是元．

查看解析收藏纠错

+选题
16. 如图，点A ， B ， C为平面内不在同一直线上的三点．点D为平面内一个动点．线段AB ， BC ， CD ， DA的中点分别为M ， N ， P ， Q ．在点D的运动过程中，有下列结论：①存在无数个中点四边形MNPQ是平行四边形；②存在无数个中点四边形MNPQ是菱形；③存在无数个中点四边形MNPQ是矩形；④存在两个中点四边形MNPQ是正方形．所有正确结论的序号是．

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 解不等式组 $\text{[math]}$ ．

查看解析收藏纠错

+选题
19. 已知：关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根．

（1）求 $\text{[math]}$ 的取值范围；

（2）若该方程有两个实数根，取一个 $\text{[math]}$ 的值，求此时该方程的根．

查看解析收藏纠错

+选题
20. 已知线段 $\text{[math]}$ ，直线 $\text{[math]}$ 垂直平分 $\text{[math]}$ 且交 $\text{[math]}$ 于点 $\text{[math]}$ ．以 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作弧，交直线 $\text{[math]}$ 于 $\text{[math]}$ 两点，分别连接 $\text{[math]}$ ．

（1）根据题意，补全图形；

（2）求证：四边形 $\text{[math]}$ 为正方形．

查看解析收藏纠错

+选题
21. 国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出：公民科学素质是实施创新驱动发展战略的基础，是国家综合国力的体现．《方案》明确提出，2020年要将我国公民科学素质的数值提升到10%以上．为了解我国公民科学素质水平及发展状况，中国科协等单位已多次组织了全国范围的调查，以下是根据调查结果整理得到的部分信息．注：科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比．
$\text{[math]}$ .2015和2018年我国各直辖市公民科学素质发展状况统计图如下：

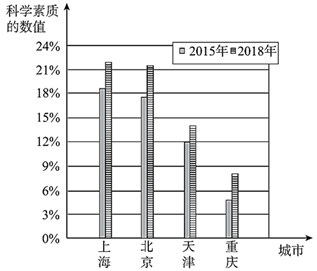
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下：

2015年

2018年

男

$\text{[math]}$

$\text{[math]}$

女

$\text{[math]}$

$\text{[math]}$

c.2001年以来我国公民科学素质水平发展统计图如下：

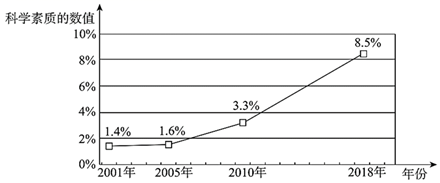
根据以上信息，回答下列问题：

（1）在我国四个直辖市中，从2015年到2018年，公民科学素质水平增幅最大的城市是，公民科学素质水平增速最快的城市是．注：科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值；科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值．

（2）已知在2015年的调查样本中，男女公民的比例约为1：1，则2015年我国公民的科学素质水平为%(结果保留一位小数)；由计算可知．在2018年的调查样本中．男性公民人数女性公民人数(填“多于”、“等于”或“少于”)．

（3）根据截至2018年的调查数据推断，你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由．

查看解析收藏纠错

+选题
22. 已知：△ABC为等边三角形．

（1）求作：△ABC的外接圆⊙O ．（不写作法，保留作图痕迹）

（2）射线AO交BC于点D ，交⊙O于点E ，过E作⊙O的切线EF ，与AB的延长线交于点F ．
①根据题意，将（1）中图形补全；

②求证：EF∥BC；

③若DE＝2，求EF的长．

查看解析收藏纠错

+选题
23. 如图，四边形ABCD为矩形，点E为边AB上一点，连接DE并延长，交CB的延长线于点P ，连接PA ， ∠DPA＝2∠DPC ．求证：DE＝2PA ．

查看解析收藏纠错

+选题
24. 已知：在平面直角坐标系 $\text{[math]}$ 中，对于任意的实数 $\text{[math]}$ ，直线 $\text{[math]}$ 都经过平面内一个定点 $\text{[math]}$ ．

（1）求点 $\text{[math]}$ 的坐标．

（2）反比例函数 $\text{[math]}$ 的图象与直线 $\text{[math]}$ 交于点 $\text{[math]}$ 和另外一点 $\text{[math]}$
①求 $\text{[math]}$ 的值；

②当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围

查看解析收藏纠错

+选题
25. 如图1，四边形ABCD为矩形，曲线L经过点D ．点Q是四边形ABCD内一定点，点P是线段AB上一动点，作PM⊥AB交曲线L于点M ，连接QM ．

小东同学发现：在点P由A运动到B的过程中，对于x₁＝AP的每一个确定的值，θ＝∠QMP都有唯一确定的值与其对应，x₁与θ的对应关系如表所示：

x₁＝AP

0

1

2

3

4

5

θ＝∠QMP

α

85°

130°

180°

145°

130°

小芸同学在读书时，发现了另外一个函数：对于自变量x₂在﹣2≤x₂≤2范围内的每一个值，都有唯一确定的角度θ与之对应，x₂与θ的对应关系如图2所示：

根据以上材料，回答问题：

（1）表格中α的值为．

（2）如果令表格中x₁所对应的θ的值与图2中x₂所对应的θ的值相等，可以在两个变量x₁与x₂之间建立函数关系．
①在这个函数关系中，自变量是，因变量是；（分别填入x₁和x₂）

②请在网格中建立平面直角坐标系，并画出这个函数的图象；

③根据画出的函数图象，当AP＝3.5时，x₂的值约为．

查看解析收藏纠错

+选题
26. 在平面直角坐标系 $\text{[math]}$ 中，存在抛物线 $\text{[math]}$ 以及两点 $\text{[math]}$ ．

（1）求该抛物线的顶点坐标；(用含 $\text{[math]}$ 的代数式表示)

（2）若该抛物线经过点 $\text{[math]}$ ，求此抛物线的表达式；

（3）若该抛物线与线段 $\text{[math]}$ 有公共点，结合图象，求 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
27. 已知线段AB ，过点A的射线l⊥AB ．在射线l上截取线段AC＝AB ，连接BC ，点M为BC的中点，点P为AB边上一动点，点N为线段BM上一动点，以点P为旋转中心，将△BPN逆时针旋转90°得到△DPE ， B的对应点为D ， N的对应点为E ．

（1）当点N与点M重合，且点P不是AB中点时，
①据题意在图中补全图形；

②证明：以A ， M ， E ， D为顶点的四边形是矩形．

（2）连接EM ．若AB＝4，从下列3个条件中选择1个：
①BP＝1，②PN＝1，③BN＝ $\text{[math]}$ ，

当条件 ▲ （填入序号）满足时，一定有EM＝EA ，并证明这个结论．

查看解析收藏纠错

+选题
28. 如果 $\text{[math]}$ 的两个端点 $\text{[math]}$ 分别在 $\text{[math]}$ 的两边上(不与点 $\text{[math]}$ 重合)，并且 $\text{[math]}$ 除端点外的所有点都在 $\text{[math]}$ 的内部，则称 $\text{[math]}$ 是 $\text{[math]}$ 的“连角弧”．

（1）图1中， $\text{[math]}$ 是直角， $\text{[math]}$ 是以 $\text{[math]}$ 为圆心，半径为1的“连角弧”．

①图中 $\text{[math]}$ 的长是，并在图中再作一条以 $\text{[math]}$ 为端点、长度相同的“连角弧”；

②以 $\text{[math]}$ 为端点，弧长最长的“连角弧”的长度是．

（2）如图2，在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，若 $\text{[math]}$ 是半圆，也是 $\text{[math]}$ 的“连角弧”，求 $\text{[math]}$ 的取值范围．

（3）如图3，已知点 $\text{[math]}$ 分别在射线 $\text{[math]}$ 上， $\text{[math]}$ 是 $\text{[math]}$ 的“连角弧”，且 $\text{[math]}$ 所在圆的半径为 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题

	2015年	2018年
男	$\text{[math]}$	$\text{[math]}$
女	$\text{[math]}$	$\text{[math]}$

x₁＝AP	0	1	2	3	4	5
θ＝∠QMP	α	85°	130°	180°	145°	130°

北京市通州区2020年中考数学一模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨