2016年甘肃省兰州市中考数学试卷（A卷）

修改时间：2024-07-12 浏览次数：1288 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1.
如图是由5个大小相同的正方体组成的几何体，则该几何体的主视图是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
2. 反比例函数是y= $\text{[math]}$ 的图象在（　　）

A . 第一、二象限 B . 第一、三象限 C . 第二、三象限 D . 第二、四象限

查看解析收藏纠错

+选题
3. 已知△ABC∽△DEF，若△ABC与△DEF的相似比为 $\text{[math]}$ ，则△ABC与△DEF对应中线的比为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 在Rt△ABC中，∠C=90°，sinA= $\text{[math]}$ ，BC=6，则AB=（　　）

A . 4 B . 6 C . 8 D . 10

查看解析收藏纠错

+选题
5. 一元二次方程x²+2x+1=0的根的情况（　　）

A . 有一个实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 没有实数根

查看解析收藏纠错

+选题
6.
如图，在△ABC中，DE∥BC，若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ =（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7.
如图，在⊙O中，若点C是 $\text{[math]}$ 的中点，∠A=50°，则∠BOC=（　　）

A . 40° B . 45° C . 50° D . 60°

查看解析收藏纠错

+选题
8. 二次函数y=x²﹣2x+4化为y=a（x﹣h）²+k的形式，下列正确的是（　　）

A . y=（x﹣1）²+2 B . y=（x﹣1）²+3 C . y=（x﹣2）²+2 D . y=（x﹣2）²+4

查看解析收藏纠错

+选题
9.
公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m² ，求原正方形空地的边长．设原正方形的空地的边长为xm，则可列方程为（　　）

A . （x+1）（x+2）=18 B . x²﹣3x+16=0 C . （x﹣1）（x﹣2）=18 D . x²+3x+16=0

查看解析收藏纠错

+选题
10.
如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（　　）

A . 45° B . 50° C . 60° D . 75°

查看解析收藏纠错

+选题
11. 点P₁（﹣1，y₁），P₂（3，y₂），P₃（5，y₃）均在二次函数y=﹣x²+2x+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（　　）

A . y₃＞y₂＞y₁ B . y₃＞y₁=y₂ C . y₁＞y₂＞y₃ D . y₁=y₂＞y₃

查看解析收藏纠错

+选题
12.
如图，用一个半径为5cm的定滑轮带动重物上升，滑轮上一点P旋转了108°，假设绳索（粗细不计）与滑轮之间没有滑动，则重物上升了（　　）

A . πcm B . 2πcm C . 3πcm D . 5πcm

查看解析收藏纠错

+选题
13.
二次函数y=ax²+bx+c的图象如图所示，对称轴是直线x=﹣1，有以下结论：①abc＞0；②4ac＜b²；③2a+b=0；④a﹣b+c＞2．其中正确的结论的个数是（　　）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
14.
如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD=2 $\text{[math]}$ ，DE=2，则四边形OCED的面积（　　）

A . 2 $\text{[math]}$ B . 4 C . 4 $\text{[math]}$ D . 8

查看解析收藏纠错

+选题
15.
如图，A，B两点在反比例函数y= $\text{[math]}$ 的图象上，C、D两点在反比例函数y= $\text{[math]}$ 的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF= $\text{[math]}$ ，则k₂﹣k₁=（　　）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . 6

查看解析收藏纠错

+选题

二、填空题

16. 二次函数y=x²+4x﹣3的最小值是．

查看解析收藏纠错

+选题
17. 一个不透明的口袋里装有若干除颜色外其他完全相同的小球，其中有6个黄球，将口袋中的球摇匀，从中任意摸出一个球记下颜色后再放回，通过大量重复上述实验后发现，摸到黄球的频率稳定在30%，由此估计口袋中共有小球个．

查看解析收藏纠错

+选题
18. 双曲线y= $\text{[math]}$ 在每个象限内，函数值y随x的增大而增大，则m的取值范围是．

查看解析收藏纠错

+选题
19. ▱ABCD的对角线AC与BD相交于点O，且AC⊥BD，请添加一个条件：，使得▱ABCD为正方形．

查看解析收藏纠错

+选题
20.
对于一个矩形ABCD及⊙M给出如下定义：在同一平面内，如果矩形ABCD的四个顶点到⊙M上一点的距离相等，那么称这个矩形ABCD是⊙M的“伴侣矩形”．如图，在平面直角坐标系xOy中，直线l：y= $\text{[math]}$ x﹣3交x轴于点M，⊙M的半径为2，矩形ABCD沿直线运动（BD在直线l上），BD=2，AB∥y轴，当矩形ABCD是⊙M的“伴侣矩形”时，点C的坐标为．

查看解析收藏纠错

+选题

三、解答题

21. 计算

（1） $\text{[math]}$ +（ $\text{[math]}$ ）^﹣¹﹣2cos45°﹣（π﹣2016）⁰

（2） 2y²+4y=y+2．

查看解析收藏纠错

+选题
22.
如图，已知⊙O，用尺规作⊙O的内接正四边形ABCD．（写出结论，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）

查看解析收藏纠错

+选题
23.
小明和小军两人一起做游戏，游戏规则如下：每人从1，2，…，8中任意选择一个数字，然后两人各转动一次如图所示的转盘（转盘被分为面积相等的四个扇形），两人转出的数字之和等于谁事先选择的数，谁就获胜；若两人转出的数字之和不等于他们各自选择的数，就在做一次上述游戏，直至决出胜负．若小军事先选择的数是5，用列表或画树状图的方法求他获胜的概率．

查看解析收藏纠错

+选题
24.
如图，一垂直于地面的灯柱AB被一钢筋CD固定，CD与地面成45°夹角（∠CDB=45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

查看解析收藏纠错

+选题
25. 阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题是，有如下思路：连接AC．
结合小敏的思路作答

（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决一下问题：

（2）如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

查看解析收藏纠错

+选题
26.
如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ $\text{[math]}$ ，1）在反比例函数y= $\text{[math]}$ 的图象上．

（1）求反比例函数y= $\text{[math]}$ 的表达式；

（2）在x轴的负半轴上存在一点P，使得S_△_AOP= $\text{[math]}$ S_△_AOB ，求点P的坐标；

（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．

查看解析收藏纠错

+选题
27.
如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OD⊥AB于点O，分别交AC、CF于点E、D，且DE=DC．

（1）求证：CF是⊙O的切线；

（2）若⊙O的半径为5，BC= $\text{[math]}$ ，求DE的长．

查看解析收藏纠错

+选题
28.
如图1，二次函数y=﹣x²+bx+c的图象过点A（3，0），B（0，4）两点，动点P从A出发，在线段AB上沿A→B的方向以每秒2个单位长度的速度运动，过点P作PD⊥y于点D，交抛物线于点C．设运动时间为t（秒）．

（1）求二次函数y=﹣x²+bx+c的表达式；

（2）连接BC，当t= $\text{[math]}$ 时，求△BCP的面积；

（3）
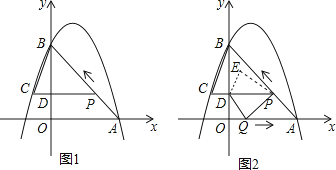
如图2，动点P从A出发时，动点Q同时从O出发，在线段OA上沿O→A的方向以1个单位长度的速度运动．当点P与B重合时，P、Q两点同时停止运动，连接DQ，PQ，将△DPQ沿直线PC折叠得到△DPE．在运动过程中，设△DPE和△OAB重合部分的面积为S，直接写出S与t的函数关系及t的取值范围．

查看解析收藏纠错

+选题

2016年甘肃省兰州市中考数学试卷（A卷）

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨