山西省运城市运康中学校2020-2021学年九年级上学期数学11月月考试卷

1. 如图所示的几何体，它的左视图是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
2. 在阳光照射下的升旗广场的旗杆从上午九点到十一点的影子长的变化规律为（）

A . 逐渐变长 B . 逐渐变短 C . 影子长度不变 D . 影子长短变化无规律

查看解析收藏纠错

+选题
3. 在同一时刻的阳光下，身高1.6 m的小强的影长是1.2 m，旗杆的影长是15 m，则旗杆的高为（）

A . 16 m B . 18 m C . 20 m D . 22 m

查看解析收藏纠错

+选题
4. 已知反比例函数 $\text{[math]}$ 的图象经过点(m，3m)，则此反比例函数的图象在（）

A . 第一、二象限 B . 第一、三象限 C . 第二、四象限 D . 第三、四象限

查看解析收藏纠错

+选题
5. 已知电压U、电流I、电阻R三者之间的关系式为： $\text{[math]}$ （或者 $\text{[math]}$ ），实际生活中，由于给定已知量不同，因此会有不同的可能图象，图象不可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 如图， $\text{[math]}$ 交双曲线 $\text{[math]}$ 于点A ，且 $\text{[math]}$ ，若矩形 $\text{[math]}$ 的面积是8，且 $\text{[math]}$ 轴，则k的值是（）

A . 18 B . 50 C . 12 D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 下列各点中，在反比例函数 $\text{[math]}$ 图象上的是（）

A . （－1，8） B . （－2，4） C . （1，7） D . （2，4）

查看解析收藏纠错

+选题
8. 如图，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的两点，过 $\text{[math]}$ 两点分别作 $\text{[math]}$ 轴的平行线交双曲线 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 有一个装有水的容器，如图所示．容器内的水面高度是10cm，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的函数关系是（）

A . 正比例函数关系 B . 一次函数关系 C . 二次函数关系 D . 反比例函数关系

查看解析收藏纠错

+选题
10. 如图，点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ ，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于点 $\text{[math]}$ ，则 $\text{[math]}$ （n为正整数）的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 在函数 $\text{[math]}$ 中，自变量x的取值范围是．

查看解析收藏纠错

+选题
12. 一次函数 $\text{[math]}$ $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ $\text{[math]}$ 的图象的两个交点分别是 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
13. 如图，方桌正上方的灯泡（看作一个点）发出的光线照射方桌后，在地面上形成阴影（正方形）示意图，已知方桌边长1.2 m，桌面离地面1.2 m，灯泡离地面3.6 m，则地面上阴影部分的面积为．

查看解析收藏纠错

+选题
14. 如图，请你添加一个条件使得 $\text{[math]}$ ．这个条件是：．

查看解析收藏纠错

+选题
15. 如图，矩形ABCD中，AB＝4，AD＝6，点E为AD中点，点P为线段AB上一个动点，连接EP，将△APE沿PE折叠得到△FPE，连接CE，CF，当△ECF为直角三角形时，AP的长为.

查看解析收藏纠错

+选题

16. 如图，楼房和旗杆在路灯下的影子如图所示．试确定路灯灯泡的位置，再作出小树在路灯下的影子．（不写作法，保留作图痕迹）

查看解析收藏纠错

+选题
17. 已知A(n，-2)，B(1，4)是一次函数y=kx+b的图象和反比例函数y= $\text{[math]}$ 的图象的两个交点，直线AB与y轴交于点C.

（1）求反比例函数和一次函数的关系式；

（2）求△AOC的面积；

（3）求不等式kx+b- $\text{[math]}$ <0的解集(直接写出答案).

查看解析收藏纠错

+选题
18.
我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x(小时)变化的函数图象，其中BC段是双曲线y= $\text{[math]}$ 的一部分．请根据图中信息解答下列问题：

（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？

（2）求k的值；

（3）当棚内温度不低于16℃时，该蔬菜能够快速生长，请问这天该蔬菜能够快速生长多长时间？

查看解析收藏纠错

+选题
19. 现有三张不透明的卡片，其中两张卡片的正面图案为“神舟首飞”，第三张卡片的正面图案为“保卫和平”，卡片除正面图案不同外，其余均相同．将这三张卡片背面向上洗匀，从中随机抽取一张，记录图案后放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求两次抽出的卡片上的图案都是“保卫和平”的概率．（图案为“神舟首飞”的两张卡片分别记为 $\text{[math]}$ 、 $\text{[math]}$ ，图案为“保卫和平”的卡片记为B）

查看解析收藏纠错

+选题
20. “父母恩深重，恩怜无歇时”，每年5月的第二个星期日即为母亲节，节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们．

（1）经过和花店卖家议价，可在原标价的基础上打八折购进，若在花店购买80个礼盒最多花费7680元，请求出每个礼盒在花店的最高标价；（用不等式解答）

（2）后来学生会了解到通过“大众点评”或“美团”同城配送会在（1）中花店最高售价的基础上降价25%，学生会计划在这两个网站上分别购买相同数量的礼盒，但实际购买过程中，“大众点评”网上的购买价格比原有价格上涨 $\text{[math]}$ m%，购买数量和原计划一样：“美团”网上的购买价格比原有价格下降了 $\text{[math]}$ m元，购买数量在原计划基础上增加15m%，最终，在两个网站的实际消费总额比原计划的预算总额增加了 $\text{[math]}$ m%，求出m的值．

查看解析收藏纠错

+选题
21. 如图，在长方形ABCD中，AB＝8，BC＝6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE＝OD．

（1）试证明DG＝EP；

（2）求AP的长．

查看解析收藏纠错

+选题
22.

（1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．

（2）结论应用：①如图2，点M，N在反比例函数 $\text{[math]}$ （k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．
②若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断MN与EF是否平行？请说明理由.

查看解析收藏纠错

+选题
23. 综合与实践
在线上教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动﹣﹣折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．

实践发现：

对折矩形纸片ABCD ，使AD与BC重合，得到折痕EF ，把纸片展平；再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B ，得到折痕BM ，把纸片展平，连接AN ，如图①．

（1）折痕BM（填“是”或“不是”）线段AN的垂直平分线；请判断图中
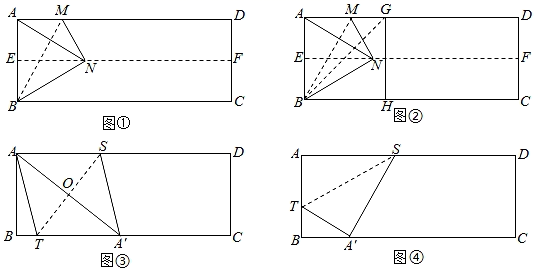
△ABN是什么特殊三角形？答：；进一步计算出∠MNE＝°；

（2）继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B ，得到折痕BG ，把纸片展平，如图②，则∠GBN＝°；
拓展延伸：

（3）如图③，折叠矩形纸片ABCD ，使点A落在BC边上的点A'处，并且折痕交BC边于点T ，交AD边于点S ，把纸片展平，连接AA'交ST于点O ，连接AT ．
求证：四边形SATA'是菱形．

解决问题：

（4）如图④，矩形纸片ABCD中，AB＝10，AD＝26，折叠纸片，使点A落在BC边上的点A'处，并且折痕交AB边于点T ，交AD边于点S ，把纸片展平．同学们小组讨论后，得出线段AT的长度有4，5，7，9．请写出以上4个数值中你认为正确的数值．

查看解析收藏纠错

+选题

山西省运城市运康中学校2020-2021学年九年级上学期数学11月月考试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

山西省运城市运康中学校2020-2021学年九年级上学期数学11月月考试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨