2017年江苏省淮安市中考数学试卷

修改时间：2024-07-12 浏览次数：2095 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. ﹣2的相反数是（）

A . 2 B . ﹣2 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 2016年某市用于资助贫困学生的助学金总额是9680000元，将9680000用科学记数法表示为（）

A . 96.8×10⁵ B . 9.68×10⁶ C . 9.68×10⁷ D . 0.968×10⁸

查看解析收藏纠错

+选题
3. 计算a²•a³的结果是（）

A . 5a B . 6a C . a⁶ D . a⁵

查看解析收藏纠错

+选题
4. 点P（1，﹣2）关于y轴对称的点的坐标是（）

A . （1，2） B . （﹣1，2） C . （﹣1，﹣2） D . （﹣2，1）

查看解析收藏纠错

+选题
5. 下列式子为最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 九年级（1）班15名男同学进行引体向上测试，每人只测一次，测试结果统计如下：
引体向上数/个
0
1
2
3
4
5
6
7
8
人数
1
1
2
1
3
3
2
1
1
这15名男同学引体向上数的中位数是（）

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题
7. 若一个三角形的两边长分别为5和8，则第三边长可能是（）

A . 14 B . 10 C . 3 D . 2

查看解析收藏纠错

+选题
8. 如图，在矩形纸片ABCD中，AB=3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AC的长是（）

A . $\text{[math]}$ B . 6 C . 4 D . 5

查看解析收藏纠错

+选题

二、填空题

9. 分解因式：ab﹣b²=．

查看解析收藏纠错

+选题
10. 计算：2（x﹣y）+3y=．

查看解析收藏纠错

+选题
11. 若反比例函数y=﹣ $\text{[math]}$ 的图象经过点A（m，3），则m的值是．

查看解析收藏纠错

+选题
12. 方程 $\text{[math]}$ =1的解是．

查看解析收藏纠错

+选题
13. 一枚质地均匀的骰子的6个面上分别刻有1〜6的点数，抛掷这枚骰子1次，向上一面的点数是4的概率是．

查看解析收藏纠错

+选题
14. 若关于x的一元二次方程x²﹣x+k+1=0有两个不相等的实数根，则k的取值范围是．

查看解析收藏纠错

+选题
15. 如图，直线a∥b，∠BAC的顶点A在直线a上，且∠BAC=100°．若∠1=34°，则∠2=°．

查看解析收藏纠错

+选题
16. 如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4：3：5，则∠D的度数是°．

查看解析收藏纠错

+选题
17. 如图，在Rt△ABC中，∠ACB=90°，点D，E分别是AB，AC的中点，点F是AD的中点．若AB=8，则EF=．

查看解析收藏纠错

+选题
18. 将从1开始的连续自然数按一下规律排列：
第1行

1

第2行

2
3
4

第3行

9
8
7
6
5

第4行

10
11
12
13
14
15
16

第5行
25
24
23
22
21
20
19
18
17
…
则2017在第行．

查看解析收藏纠错

+选题

三、解答题

19. 计算题

（1） |﹣3|﹣（ $\text{[math]}$ +1）⁰+（﹣2）²；

（2）（1﹣ $\text{[math]}$ ）÷ $\text{[math]}$ ．

查看解析收藏纠错

+选题
20. 解不等式组： $\text{[math]}$ 并写出它的整数解．

查看解析收藏纠错

+选题
21. 已知：如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：△ADE≌△CBF．

查看解析收藏纠错

+选题
22. 一只不透明的袋子中装有2个白球和1个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．

（1）用树状图或列表等方法列出所有可能出现的结果；

（2）求两次摸到的球的颜色不同的概率．

查看解析收藏纠错

+选题
23. 某校计划成立学生社团，要求每一位学生都选择一个社团，为了了解学生对不同社团的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查，规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项，并将统计结果绘制了如下两个不完整的统计图表．
社团名称
人数
文学社团
18
科技社团
a
书画社团
45
体育社团
72
其他
b
请解答下列问题：

（1） a=，b=；

（2）在扇形统计图中，“书画社团”所对应的扇形圆心角度数为；

（3）若该校共有3000名学生，试估计该校学生中选择“文学社团”的人数．

查看解析收藏纠错

+选题
24. A，B两地被大山阻隔，若要从A地到B地，只能沿着如图所示的公路先从A地到C地，再由C地到B地．现计划开凿隧道A，B两地直线贯通，经测量得：∠CAB=30°，∠CBA=45°，AC=20km，求隧道开通后与隧道开通前相比，从A地到B地的路程将缩短多少？（结果精确到0.1km，参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732）

查看解析收藏纠错

+选题
25. 如图，在△ABC中，∠ACB=90°，O是边AC上一点，以O为圆心，OA为半径的圆分别交AB，AC于点E，D，在BC的延长线上取点F，使得BF=EF，EF与AC交于点G．

（1）试判断直线EF与⊙O的位置关系，并说明理由；

（2）若OA=2，∠A=30°，求图中阴影部分的面积．

查看解析收藏纠错

+选题
26. 某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线ABCD表示人均收费y（元）与参加旅游的人数x（人）之间的函数关系．

（1）当参加旅游的人数不超过10人时，人均收费为元；

（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？

查看解析收藏纠错

+选题
27. 【操作发现】
如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．

（1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；

（2）在（1）所画图形中，∠AB′B=．

（3）【问题解决】
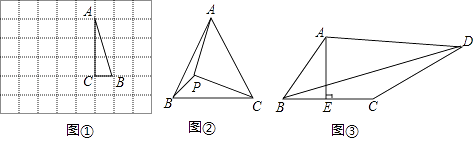
如图②，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．
小明同学通过观察、分析、思考，对上述问题形成了如下想法：
想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；
想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．
…
请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）

（4）【灵活运用】
如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示）．

查看解析收藏纠错

+选题
28. 如图①，在平面直角坐标系中，二次函数y=﹣ $\text{[math]}$ x²+bx+c的图象与坐标轴交于A，B，C三点，其中点A的坐标为（﹣3，0），点B的坐标为（4，0），连接AC，BC．动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒．连接PQ．

（1）填空：b=，c=；

（2）在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；

（3）在x轴下方，该二次函数的图象上是否存在点M，使△PQM是以点P为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由；

（4）如图②，点N的坐标为（﹣ $\text{[math]}$ ，0），线段PQ的中点为H，连接NH，当点Q关于直线NH的对称点Q′恰好落在线段BC上时，请直接写出点Q′的坐标．

查看解析收藏纠错

+选题

第1行					1
第2行				2	3	4
第3行			9	8	7	6	5
第4行		10	11	12	13	14	15	16
第5行	25	24	23	22	21	20	19	18	17

社团名称	人数
文学社团	18
科技社团	a
书画社团	45
体育社团	72
其他	b

引体向上数/个	0	1	2	3	4	5	6	7	8
人数	1	1	2	1	3	3	2	1	1

2017年江苏省淮安市中考数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨