修改时间:2024-07-13 浏览次数:217 类型:期末考试


如图①,在正方形ABCD中,∠MAN=45°,点M、N分别在边BC、CD上.求证:MN=BM+DN.
证明思路如下:
第一步:如图②,将 绕点A按顺时针方向旋转90°得到△ABE,再证明E、B、M三点在一条直线上.
第二步:证明 .
请你按照证明思路写出完整的证明过程.
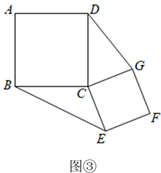
如图③,四边形ABCD和CEFG为正方形,连接DG、BE,得到 和
.
下列关于这两个三角形的结论:①周长相等; ②面积相等; ③∠CBE=∠CDG.
其中所有正确结论的序号是.
如图④,分别以▱ABCD的四条边为边向外作正方形,连接EF,GH,IJ,KL.若▱ABCD的面积为8,则图中阴影部分(四个三角形)的面积之和为.
试题篮