新疆昌吉市2020年数学中考四模试卷

1. -2的相反数是( )

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 自然界中的数学不胜枚举，如蜜蜂建造的蜂房既坚固又省料，其厚度为0.0073厘米，将0.0073用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图，将一块含有 $\text{[math]}$ 的直角三角板的顶点放在直尺的一边上，若 $\text{[math]}$ ，那么 $\text{[math]}$ 的度数是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

5. 为了解学生课外阅读时间情况，随机收集了30名学生一天课外阅读时间，整理如下表：

阅读时间/小时	0.5及以下	0.7	0.9	1.1	1.3	1.5及以上
人数	2	9	6	5	4	4

则本次调查中阅读时间的中位数和众数分别是（）

A . 0.7和0.7 B . 0.9和0.7 C . 1和0.7 D . 0.9和1.1

查看解析收藏纠错

+选题

6. 若关于x的一元二次方程 $\text{[math]}$ 有两个实数根，则k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在△ABC中，点D ， E分别在AB ， AC上，DE∥BC ， AD=CE ．若AB：AC=3：2，BC=10，则DE的长为（　　）

A . 3 B . 4 C . 5 D . 6

查看解析收藏纠错

+选题
8. 如图，在矩形ABCD中，点F在AD上，点E在BC上，把矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为 $\text{[math]}$ 且∠AFG=60°，GE=2BG，则折痕EF的长为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，四边形 $\text{[math]}$ 内接于半圆O， $\text{[math]}$ 为直径， $\text{[math]}$ ，过点D作 $\text{[math]}$ 于点E，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点F.若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 8 B . 10 C . 15 D . 24

查看解析收藏纠错

+选题

10. 分解因式： $\text{[math]}$ =

查看解析收藏纠错

+选题
11. 分式方程 $\text{[math]}$ 的解为.

查看解析收藏纠错

+选题
12. 圆锥的侧面展开图是一个弧长为6π的扇形，则这个圆锥底面半径是.

查看解析收藏纠错

+选题
13. 如图，在Rt△ABC中，∠C＝90°，以顶点B为圆心，适当长度为半径画弧，分别交AB，BC于点M，N，再分别以点M，N为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧交于点P，作射线BP交AC于点D.若∠A＝30°，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
14. 如图，Rt△AOB中，∠AOB＝90°，顶点A，B分别在反比例函数y＝ $\text{[math]}$ （x＞0）与y＝ $\text{[math]}$ （x＜0）的图象上，则tan∠BAO的值为 .

查看解析收藏纠错

+选题
15. 如图，抛物线y=ax²+bx+c的对称轴是x=﹣1.且过点 $\text{[math]}$ ，有下列结论：
①abc $\text{[math]}$ 0； ②a﹣2b+4c=0； ③25a﹣10b+4c=0； ④3b+2c $\text{[math]}$ 0； ⑤a﹣b≥m（am﹣b）；

其中所有正确的结论是.（填写正确结论的序号）

查看解析收藏纠错

+选题

16. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
17. 先化简，再求值： $\text{[math]}$ ，其中x的值从不等式组 $\text{[math]}$ 的整数解中选取.

查看解析收藏纠错

+选题

18. 现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：

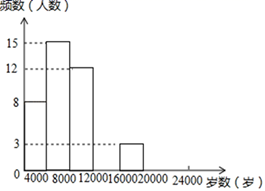
步数	频数	频率
0≤x＜4000	8	a
4000≤x＜8000	15	0.3
8000≤x＜12000	12	b
12000≤x＜16000	c	0.2
16000≤x＜20000	3	0.06
20000≤x＜24000	d	0.04

请根据以上信息，解答下列问题：

（1）写出a，b，c，d的值并补全频数分布直方图；

（2）本市约有37600名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，求被选取的两名教师恰好不在同一组的概率.

查看解析收藏纠错

+选题

19. 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）证明：G是 $\text{[math]}$ 中点；

（2）连接 $\text{[math]}$ ，证明： $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 图①是放置在水平面上的台灯，图②是其侧面示意图（台灯底座高度忽略不计），其中灯臂AC＝44cm，灯罩CD＝32cm，灯臂与底座构成的∠CAB＝60°.CD可以绕点C上下调节一定的角度.使用发现：当CD与水平线所成的角为30°时，台灯光线最佳.现测得点D到桌面的距离为54.06cm.请通过计算说明此时台灯光线是否为最佳？（参考数据： $\text{[math]}$ 取1.73）.

查看解析收藏纠错

+选题
21. 一名在校大学生利用“互联网+”自主创业，销售一种产品，这种产品的成本价10元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元/件，市场调查发现，该产品每天的销售量 $\text{[math]}$ （件 $\text{[math]}$ 与销售价 $\text{[math]}$ （元/件）之间的函数关系如图所示．

（1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出自变量 $\text{[math]}$ 的取值范围；

（2）求每天的销售利润W（元 $\text{[math]}$ 与销售价 $\text{[math]}$ （元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

查看解析收藏纠错

+选题
22. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的⊙O交 $\text{[math]}$ 于点D，切线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
23. 如图，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ 、 $\text{[math]}$ ，与y轴交于点C.

（1）求二次函数的解析式；

（2）若点P为抛物线上的一点，点 $\text{[math]}$ 为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点 $\text{[math]}$ 的坐标；

（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线 $\text{[math]}$ 于点D，求四边形 $\text{[math]}$ 面积的最大值及此时点E的坐标.

查看解析收藏纠错

+选题

新疆昌吉市2020年数学中考四模试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

新疆昌吉市2020年数学中考四模试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨