修改时间:2024-07-13 浏览次数:262 类型:中考模拟
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
经抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
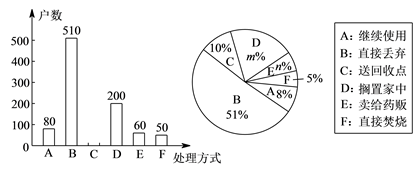
|
销售方式 |
粗加工后销售 |
精加工后销售 |
|
每吨获利(元) |
1000 |
2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
试题篮