修改时间:2024-11-06 浏览次数:391 类型:中考模拟
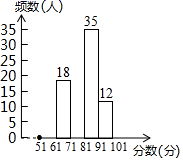
| 分数段(分) | 频数(人) | 频率 |
| | | 0.1 |
| | 18 | 0.18 |
| | | |
| | 35 | 0.35 |
| | 12 | 0.12 |
| 合计 | 100 | 1 |
如图1,已知在 ,
,
,
,点
为
边上的一个动点,连接
.设
,
.
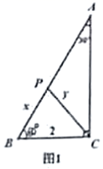
当 时,则①
,②
;
试求y与x之间的函数关系式并写出自变量 的取值范围;
| | 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| | 2 | 1.8 | 1.7 | _ | 2 | 2.3 | 2.6 | 3.0 | _ |
①计算并补全表格(说明:补全表格时相关数值保留一位小数)
②建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
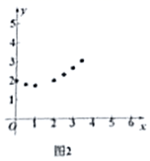
③结合画出的函数图象,写出该函数的两条性质.
试题篮